分布以数学的方式刻画变量的变差(在某个类型内部的差异)和多样性(不同类型之间的差异),将变量表示为在数值上或类别上定义的概率分布。
分布为每一个可能的结果值分配一个概率。各种统计量将分布中包含的信息压缩为单个数值,例如均值,分布的平均值。均值之外的第二个重要统计量是方差,可以衡量一个分布的离散程度,也就是数据与均值之间距离的平方的平均值。分布的标准差是另一个常用的统计量,等于方差的平方根。
正态分布的结构
正态分布的均值是对称的。正态分布的特征在于其均值和标准差(或者等价地,其方差)。也就是说所有正态分布的图形看上去都是相似的,大约68%的结果在均值的一个标准差内,大约95%的结果在两个标准差内,并且超过99%的结果在三个标准差内。正态分布允许任何大小的结果或事件,不过“大”事件是非常罕见的,与均值距离超过五个标准差的事件发生的概率为200万分之一。
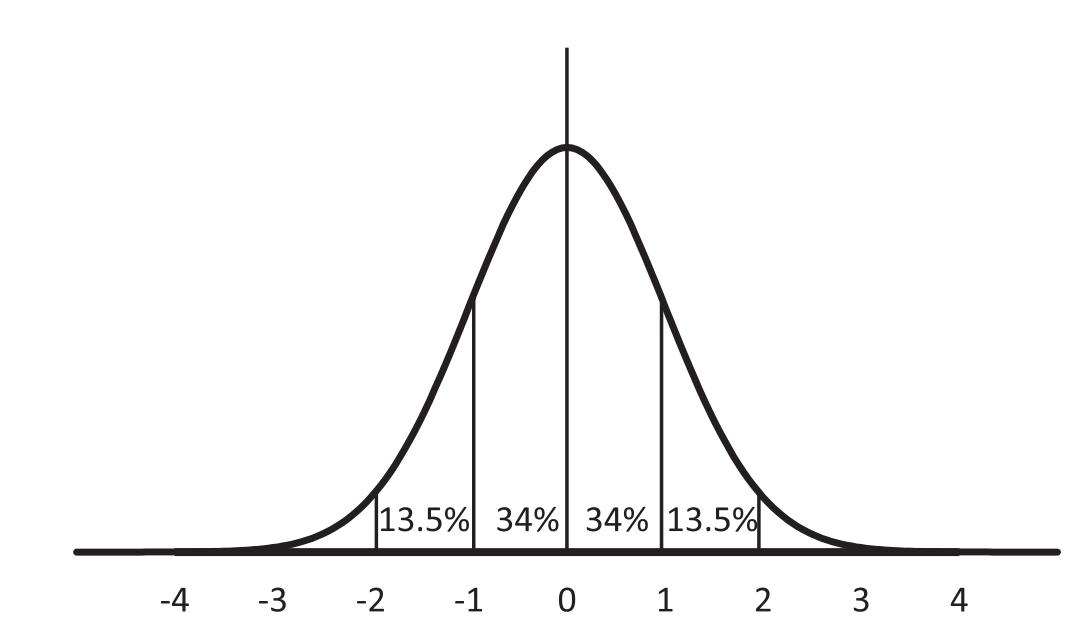
我们可以利用正态分布的规律给各种范围的结果分配概率。如果位于美国威斯康星州密尔沃基市房子的平均面积是2,000平方英尺(1平方英尺≈0.09平方米)、标准差为500平方英尺,那么那里68%的房子面积介于1,500平方英尺到2,500平方英尺之间,95%的房子面积介于1,000平方英尺到3,000平方英尺之间。
并不是所有事件的规模(大小)都是正态分布的。地震、战争死亡人数和图书销量都呈长尾分布,这种分布主要由很小的事件组成,也包括极少数非常巨大的大型事件。
中心极限定理
中心极限定理表明为什么对随机变量求和或取均值会产生正态分布。
只要各随机变量是相互独立的,每个随机变量的方差都是有限的,且没有任何一小部分随机变量贡献了大部分方差,那N≥20个随机变量的和就近似一个正态分布。均值也将是正态分布的。
中心极限定理一个非常重要的特征是,随机变量本身不一定是正态分布的。它们可以有任何分布,只要每一个随机变量都具有有限的方差,并且它们中的任何一小部分随机变量都不贡献大部分方差。
这里有好几个条件,而且只要满足其中任何一个条件就足够了。林德伯格条件(Lindeberg condition)是比较常见的一种,它要求,随着变量的数量的无限增加,来自任何一个变量的总变差的比例将收敛为零。
假设,在一个500人的小城镇中,人们的购买行为数据显示,每个人平均每个星期花费100美元。在这些人中,可能有些人这个星期只花50美元、下个星期则花150美元,另一部分人可能每3个星期花费300美元。而其他人则可能每个星期的花费在20至180美元之间。只要每个人的支出都只有有限的方差并且没有任何一小部分人贡献了大部分方差,那么分布的总和必定是一个正态分布,其均值为50,000美元。每个星期的总支出也将是对称的:可能高于55,000美元,也可能低于45,000美元
一个人的身高取决于基因、环境以及两者之间的相互作用。基因的贡献率可能高达80%,因此不妨假设身高只取决于基因。研究表明,至少180个基因有助于人体长高。3例如,一个基因可能有助于长出较长的颈部或头部,另一个基因可能有助于长出更长的胫骨。虽然基因之间存在相互作用,但我们可以假设在“长高”这件事情上,每个基因都是相互独立的。如果身高等于180个基因贡献的总和,那么身高将呈现正态分布。
另一种解释
在适当的条件下,大量相互独立随机变量的均值经适当标准化后依分布收敛于正态分布。
每次从这些总体中随机抽取 n 个抽样,一共抽 m 次。 然后把这 m 组抽样分别求出平均值, 这些平均值的分布接近正态分布。
随机变量平均值的标准差并不等于变量标准差的平均值,而且总和的标准差也不等于标准差的总和。相反,这些关系取决于总体大小的平方根。
平方根法则(The square root rules)
N个相互独立的随机变量,都具有标准差σ,对这些随机变量的均值的标准差 σμ 和对这些随机变量总和的标准差 σΣ,分别由以下公式给出:

正态分布的应用
为什么罕见结果在规模小的群体中更常见
均值的标准差公式表明,大的总体的标准差要比小的总体的标准差低得多。由此可以推断,在小的群体中应该会观察到更多的好事和更多的坏事。
最安全的居住地是小城镇,但最不安全的地方也是小城镇;肥胖率和癌症发病率最高的那些郡县的人口较少。这些事实都可以通过标准差的差异来解释。
如果不考虑样本量,直接根据离群值(异常值)推断因果关系可能会导致相当糟糕的政策行为。
现在有两所学校,一所是只有100名学生的小学校,另一所是有1 600名学生的大学校,并假设这两所学校学生的成绩均来自相同的分布,平均分为100,标准差为80。在小学校中,平均值的标准差等于8,即学生成绩的标准差80除以学生人数的平方根10。而在大学校中,平均值的标准差则等于2。如果以平均分为标准,把那些平均成绩在110以上的学校称为“优秀”,把平均成绩在120以上的学校称为“非常优秀”,那么将只有小学校才有可能达到这个标准。对于小学校而言,平均成绩为110时,只比总体均值高出了1.25个标准差,这类事件发生的概率大约为10%。而平均成绩为120时,则比总体均值高出了2.5个标准差,这类事件大约150所学校发生一次。对大学校进行相同的计算时,我们却会发现“优秀”阈值意味着比均值高5个标准差,而“非常优秀”阈值则比均值高10个标准差!实际上这类事件永远不会发生。因此,最好的那些学校普遍规模较小这个“事实”并不能证明小学校的表现更好。即便学校规模本身完全没有影响,“最好的学校都很小”这种事情也会发生,因为平方根法则会起作用。
显著性检验
利用正态分布的规律来检验各种平均值的显著性差异。如果经验均值与假设均值之间的偏差了超过两个标准差,那么社会科学家就会拒绝这两种均值相同的假设。两个标准差的阈值(5%显著性)是一个惯例。
现在提出这样一个假设,即巴尔的摩的通勤时间与洛杉矶的通勤时间相同。假设数据表明,巴尔的摩的通勤时间平均为33分钟,而洛杉矶为34分钟。如果这两个数据集的均值标准差都是1分钟,那么我们就不能拒绝巴尔的摩和洛杉矶两地通勤时间相同的假设。虽然二者的均值不同,但只存在1个标准差。如果洛杉矶的平均通勤时间为37分钟,那么我们就会拒绝这个假设,因为均值之间相差4个标准偏差。
六西格玛方法
六西格玛方法是摩托罗拉公司于20世纪80年代中期提出的,主要是为了降低标准差,这样即使出现了6个标准差的误差,也可以避免出现故障。6个标准差的含义是,误差率仅为十亿分之二。实际使用的阈值假设1.5个标准差的出现是不可避免的。那么,一个六西格玛事件实际上对应于一个四个半西格玛事件,这时允许的误差率大约为三百万分之一。
一家企业专业生产制造门把手所用的螺栓。它生产的螺栓必须天衣无缝地与其他制造商生产的旋钮组装在一起。规格要求是螺栓直径为14毫米,但是任何直径介于13毫米与15毫米之间的螺栓也可以接受。如果螺栓的直径呈正态分布,均值为14毫米,标准差为0.5毫米,那么任何超过两个标准差的螺栓都是不合格的。两个标准差事件发生的概率为5%,这个概率对于一家制造企业来说太高了。
六西格玛方法降低了标准差,这样即使出现了6个标准差的误差,也可以避免出现故障。六西格玛方法涉及缩减标准差的大小从而降低生产出不合格产品的可能性。各企业可以通过加强质量控制来降低误差率。
在生产螺栓这个例子中,就要求必须把螺栓直径的标准差减少至1/6毫米。螺栓制造企业不可能精确地测量每个螺栓的直径,它可能会抽样几百个,并根据这样一个样本来估计均值和标准差。然后通过假设直径的变差源于多种随机效应的总和,例如机器振动、金属质量变化以及压力机温度和速度的波动,就可以利用中心极限定理推断出正态分布。这样一来,这家螺栓制造企业就可以得出一个基准标准差,然后花大力气去降低它。
对数正态分布:乘法冲击
中心极限定理要求我们对随机变量求和或求平均值,以获得正态分布。如果随机变量是不可相加而是以某种方式相互作用的,或者如果它们不是相互独立的,那么产生的分布就不一定是正态分布。事实上,一般情况下都不会是。
如果将20个不均匀地分布在0到10之间的随机变量相乘,那么多次相乘后所得到的乘积将会包括一些很接近于零的结果与一些相当大的结果,从而生成如图所示的对数正态分布。
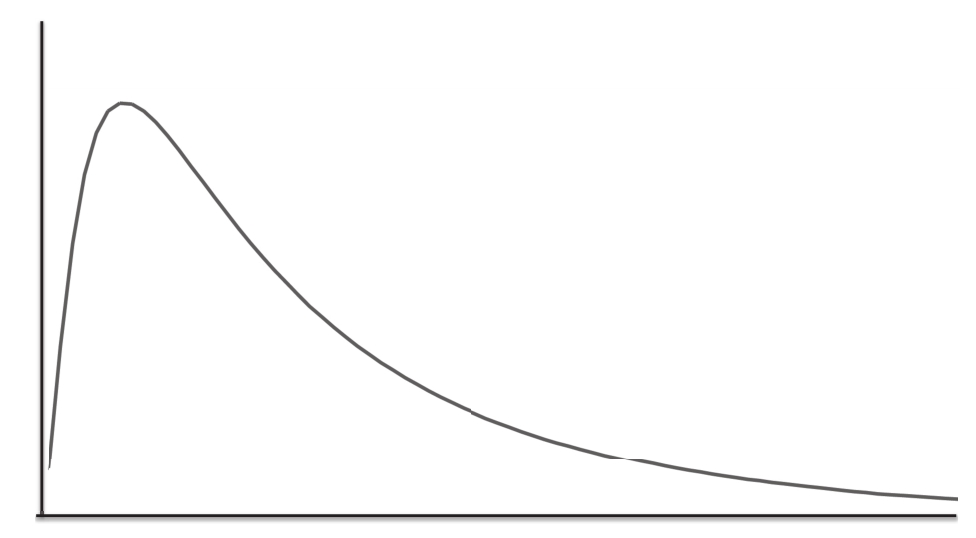
一个对数正态分布的尾部长度取决于随机变量相乘的方差。如果它们的方差很小,尾巴就会很短,如果方差很大,尾巴就可能会很长。
对数正态分布只取正值,有更长的尾巴,意味着更大的事件和更多非常小的事件。当高方差的随机变量相乘时,尾部会变得更长。长尾分布的可预测性较差,而正态分布则意味着很强的规律性。
将一组很大的数相乘会产生一个非常大的数字。在各种各样的情况下都会出现对数正态分布,包括英国农场的大小,地球上的矿物质的浓度,从受到感染到症状出现的时间,等等。大多数国家的收入分布也近似于对数正态分布,尽管在最顶端,许多点会偏离对数正态分布,因为高收入的人“太多”了。
收入分布更接近于对数正态分布而不是正态分布。大多数企业和机构都按某种百分比来分配加薪,表现高于平均水平的人能够得到更高百分比的加薪,表现低于平均水平的人则只能得到更低百分比的加薪。如果每一年的绩效都是相互独立且随机的,那么根据员工绩效按百分比加薪,就会产生一个对数正态分布。即使后来的表现相同,未来几年的收入差距也会加剧。假设一名员工因过去几年表现良好,收入水平达到了80,000美元,而另一名员工则只达到了60,000美元。在这种情况下,当这两名员工的表现同样出色并都可以获得5%的加薪时,前者能够获得4,000美元的加薪,后者却只能得到3,000美元的加薪。这就是说,尽管绩效完全相同,不平等也会导致更大的不平等。如果企业按绝对数额分配加薪,那么两名绩效相同的员工将获得相同的加薪,由此产生的收入分布将接近正态分布。