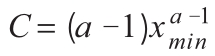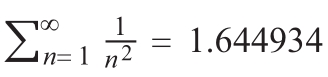幂律分布就是通常所称的长尾分布或重尾分布。在把这种分布绘制在图上时,会产生对应大事件的沿水平轴运行的长尾。
产生幂律分布要求非独立性,通常以正反馈的形式出现。
图书销售、森林火灾的发生和城市人口都不同于光顾杂货店的次数,这些并不是独立的。当某个人买了一本《哈利·波特》后,其他人也可能跟着买;当一棵树着火时,火势会蔓延到邻近的树木;当一个城市的人口增加时,这个城市的基础设施会随之改善,工作机会也会随之增加,从而对其他人更具吸引力。社会学家罗伯特·默顿(Robert Merton)把这种已经拥有更多的人未来也能够得到更多的现象称为马太效应(Matthew effect)。
幂律分布的结构
幂律分布中,事件发生的概率与事件大小的某个负指数成比例。因此,在幂律分布中,小事件的数量要比大事件要多得多。
一个定义在区间[xmin,∞)上幂律分布可以写成如下形式:
P(x)=Cx-a
指数a>1决定了尾部的长度,同时常数项确保总概率的分布。
幂律分布缺乏一个可明确定义的均值。例如,从指数为1.5的幂律分布中抽取出来的数据均值永远不会收敛。换句话说,它会无限地增加。
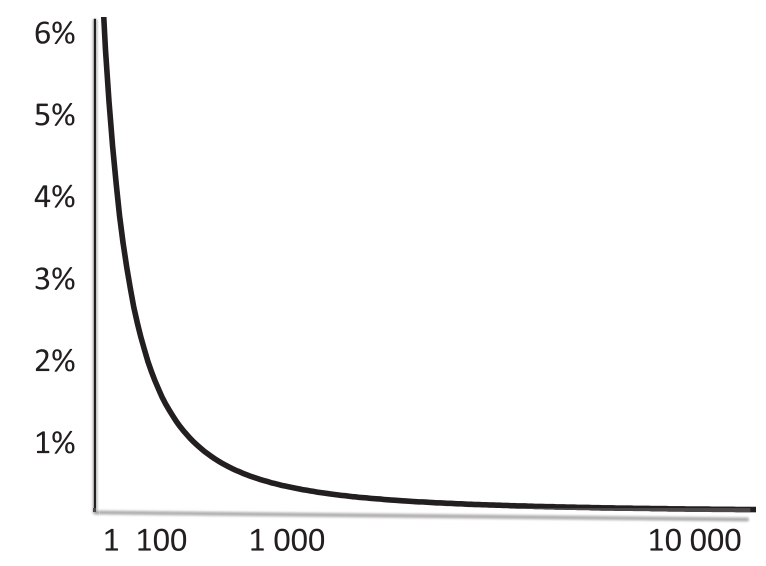
在幂律分布中,大事件虽然也很少见,但是它们发生的频率足以引起注意和准备。如果事件的概率为0.001,那么这个事件在一年内不发生的概率等于(0.999)365=0.694。因此,该事件发生的概率等于31.6%。
恐怖袭击导致x人死亡的概率大体上可以写为幂律分布p(x) = 0.608x-2。之所以选择系数0.608,是为了使概率总和等于1。因为 0.608 与 1.644934 的乘积等于1。
不是每一个长尾分布都是幂律分布。要想快速地检验某个分布是不是幂律分布,可以用双对数坐标系把该分布画出来,将幂律分布转换为直线。
齐普夫定律
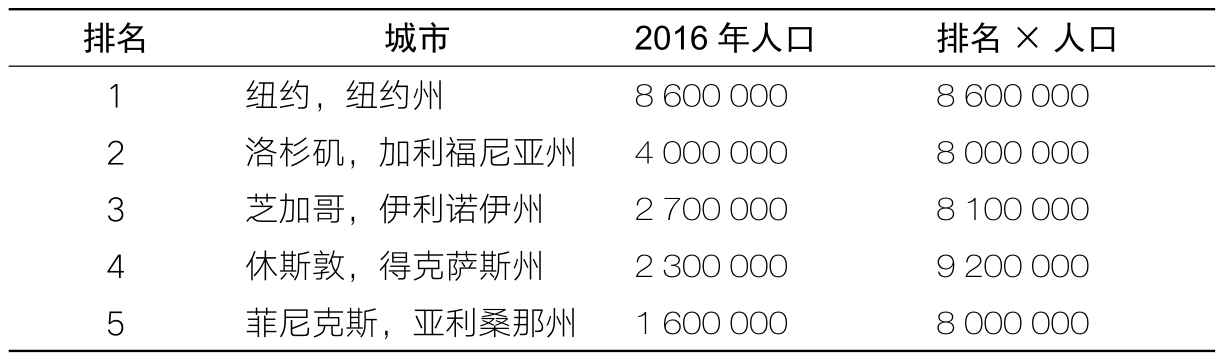
对于指数为2的幂律分布(a=2),事件的等级排列序号乘以它的大小等于常数,即:
事件等级×事件大小=常数
单词符合齐普夫定律,最常见的英语单词 the出现的频率为7%,第二最常见的英语单词 of出现的频率为3.5%。of的等级排列序号2乘以频率3.5%,恰恰等于7%。
幂律分布的逻辑
优先连接模型
一连串物体(人)一个接一个地到达。第一个到达者创建一个实体。后续每次有人到达时都应用以下规则:在概率p(较小)的情况下,新到达者创造一个新的实体;在概率(1-p)的情况下,新到达者加入现有的某个实体。加入某个特定实体的概率等于该实体的大小除以到目前为止所有到达者的数量。
想象一下大学新生进入大学校园时的情景。第一个来到学校的学生创建了一个新的社团,第二个到达的学生以较小的概率创建了自己的社团,更有可能的是,他会加入第一个学生创建的社团。前10个到达的学生可能会创建3个社团:一个有7个成员,一个有两个成员,一个有一个成员。第11个到达的学生只会以极小的概率创建第4个社团,如果不创建新的社团,她就加入现有的社团。如果这样做,那么她有70%的可能性加入已有7个学生的社团,有20%的可能性加入已有两个学生的社团,只有10%的可能性加入只有一个学生的社团。
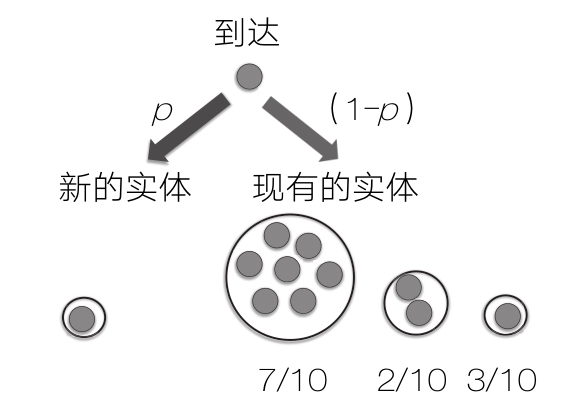
模型假设实体以相对于其比例的速度增长。优先连接模型有助于解释为什么网络链接、城市规模、企业规模、图书销量和学术引用数量的分布都是幂律分布。在这些情况下,一个行动(比如一个人购买了一本书)会增加其他人也这样做的可能性。如果从某家企业购买商品的概率与它在当前市场的份额成正比,同时如果新企业进入市场的概率较低,那么优先连接模型预测企业规模的分布将是幂律分布。同样的逻辑也适用于图书销量、音乐下载量和城市发展。
森林火灾模型 (forest fire model)
“森林”最初只是一个空的N×N网格。每个周期在网格上随机选择一个格点。如果该格点为空,那么就以概率g在那里种上一棵树。如果该格点上已经有树,那么闪电会以概率(1-g)击中该格点。如果该格点有一棵树,那么树会着火,火势会蔓延到所有连接到该格点的有树的格点。
自组织临界模型,它通过在系统中建立相互依赖关系的过程产生幂律分布,直到系统达到临界状态为止。
森林火灾模型是自组织临界模型的一种。树木可能会随机地被闪电击中。当树木的密度较低时,由闪电引发的任何火灾的规模都很小,最多只会蔓延到几个格点。当树木密度变得足够高时,再被闪电击中就会导致森林大火。森林还会树木密度自组织地达到了一个临界状态。如果密度较低,密度会增加(因为火灾很小)。如果密度超过了阈值,那么任何火灾都会毁掉整个森林。
沙堆模型(sand pile model)假设有人将沙粒从距桌面几十厘米的地方洒落到桌子上。随着沙粒不断增多,一个沙堆开始形成。最终,沙子的堆积会达到临界状态,此后每加一次沙子都可能导致“沙崩”。在这种临界状态下,多加入的沙子通常要么没有影响,要么最多只会导致一些沙子下滑。这些属于幂律分布中的数量众多的小事件。但有时,只要再加入一粒沙子就会导致大规模的“沙崩”,这就是大事件。
通过自组织达到临界状态的关键假设是压力平稳地增加,同时压力在爆发时迅速减少,这包括可能发生的大事件。
长尾分布的含义
长尾分布意味着少数几个大“赢家”(大崩溃、大地震、大火灾和严重的交通拥堵)和很多的“输家”,对公平、灾难和波动性都会产生影响。
公平
就像我们在优先连接模型中看到的,因为马太效应,正反馈创造了少数大赢家。
在市场中,要发生正反馈,人们必须知道别人买了什么商品,而且人们必须有能力购买商品。福特公司不可能无限增加卡车的产量,但是腾讯却可以无限量地提供微信程序,只要有人愿意下载。
研究者让大学生挑选和下载歌曲。在第一个实验组中,被试不知道其他人下载了哪些歌曲,下载量的分布具有较短的尾部,没有出现下载量超过200次的歌曲,且下载量少于30次的歌曲也只有一首。在第二个实验组中,被试知道其他人下载了哪些歌曲,下载量的分布具有较长的尾巴,有一首歌的下载量超过300次。而且,超过一半歌曲的下载量都不到30次。
尾巴变长了,社会影响增加了不平等。
如果社会影响只会导致人们下载更好的歌曲,那么这种不平等也不会造成什么问题。但事实上,这两个实验组的下载量之间的相关性并不强。我们可以将第一个实验组中每一首歌的下载次数解释为歌曲质量的一个表征,那么这项研究表明,社会影响并没有导致人们去下载更好的歌曲。
大赢家的出现不是随机的,但它们其实并不一定是最好的。
极端的成功本身就表明中心极限定理是不成立的。人们不会独立地购买书籍或引用论文。惊人的成功可能意味着正反馈,也许还有一点运气。
幂律分布还意味着,构成概率分布的很大一部分是非常多的小事件。这些小事件合到一起,也足以产生与大事件同等规模的经济价值。
互联网的出现,使零售商能够出售大量的书籍、电影和音乐,尽管有些东西只能吸引少数人。一个只卖一本畅销书、卖出了500万的零售商,获得的利润可能与另一个销售1万种书、每种书只卖出500本的零售商差不多。
灾难
长尾分布还包括灾难性事件:地震、火灾、金融崩溃和交通拥堵。尽管模型无法预测地震,但确实可以深入解释为什么地震的分布会满足幂律。这些相关的知识告诉我们各种强度的地震发生的可能性(地震的强烈可以用齐普夫定律来预测)。我们至少知道会发生什么,尽管不知道什么时候会发生。
波动性
如果从某家企业购买商品的概率与它在当前市场的份额成正比,同时如果新企业进入市场的概率较低,那么优先连接模型预测企业规模的分布将是幂律分布。
企业规模的分布应该会影响市场波动性。例如,我们可以将某个国家的国内生产总值视为数千家企业的总产量。如果各家企业的生产水平相互独立且变差有限,那么根据中心极限定理,这个国家的国内生产总值分布将服从正态分布。也就是说,企业生产水平的差异越大,总体波动性就越大。如果企业规模的长尾分布导致生产水平上更大的变差,那么这种长尾分布也必定与更大的总体波动性相关。
长尾分布的世界
长尾分布是由于反馈和相互依赖性而产生的。随着世界中相互联系性的提高和反馈的增加,我们应该会观察到更多的长尾分布,同时现在关注的这些长尾分布的尾部也可能会进一步拉长。这就是说,不平等可能会增加,灾难可能变得更大,波动性也会变得更加剧烈。
波士顿的中央隧道工程(Big Dig)是一条穿过市中心的长达5,000多米的隧道,这个项目花费了140亿美元(相当于最初预算的3倍多)。根据模型思维的方法,我们不会把这个项目简单地视为一个单独的项目,而是作为很多子项目的总和:挖掘深沟、浇筑混凝土隧道、设计排水系统、建造墙壁和“顶盖”。项目的总成本等于各个子项目成本的总和。
如果每个子项目的成本都是相加的,那么这个项目的成本分布将是正态分布。然而,各个子项目的成本是相互关联的。原本计划用来将顶盖黏合到位的那种环氧树脂强度不够时,就不得不用成本更高、强度更大的另一种环氧树脂来代替,从而增加了项目的成本。而且,第一种环氧树脂的失效还产生了移除和更换折叠顶盖的额外成本。这些工作反过来又需要重做项目的其他几个部分。于是总体成本增加了一倍以上,因为每个项目必须撤销然后重做。这种相互依赖性最终导致了一个大型且昂贵的事件。
搜索与机会
为什么一个人获得机会的数量可能与他的成功经历密切相关?
假设我们可能会对所选择的价值的分布有所了解,例如它的均值、标准差,以及这种分布是正态分布还是长尾分布等。
我们将职业选择建模为一个搜索过程。给定某个行业,一个人尝试某条职业道路。我们将这种行为建模为从一个分布中抽取某个事件。假设,这个人可以坚持这个职业选择或再试一次,再试一次对应于从分布中的另一次抽取。
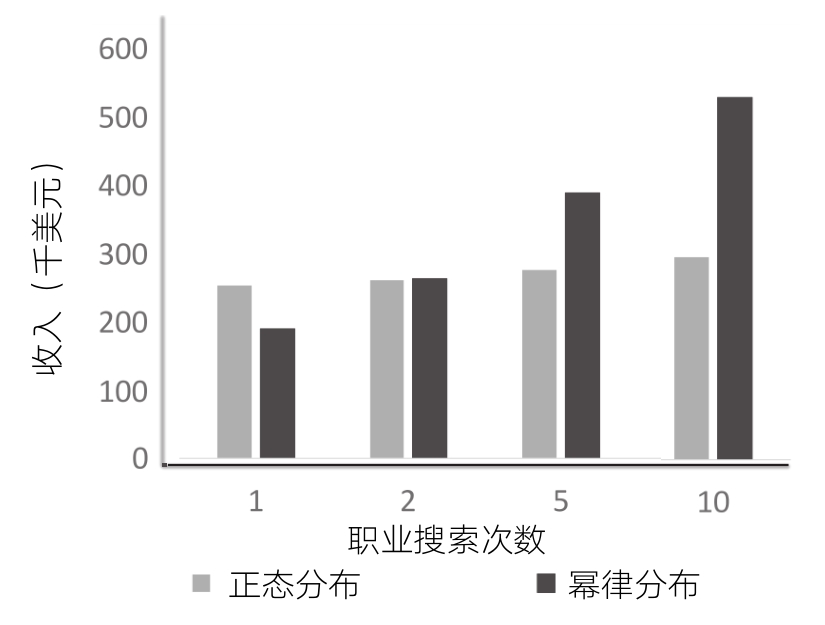
例如,考虑一个有才华的年轻科学家的职业选择。她可以选择去医学院深造,也可以选择去研究量子计算。医学院提供了一条更安全的道路,选择研究量子计算则可能成为一名创业企业家并承担更多风险。为了解释这些差异,我们将医生的工资分布表示为均值25万美元,标准差25 000美元的正态分布,并把量子计算企业家的工资分布表示为指数为3、期望工资为20万美元的幂律分布。(我们让工资分布等于随机变量x的100,000倍,其中,p(x) = 2x-3 从1到 ∞。变量x的均值等于2,因此工资分布的均值为200 000美元。)
假设在每个职业中分别进行1次、2次、5次和10次职业搜索,下图显示在20次测试中得到的平均最高工资。如果这位科学家有机会在量子计算初创企业中尝试10次,那么她的薪资将会是她选择进入医学院深造并尝试10个职业后收入的两倍。
机会的增加可以创造风险激励,这个逻辑可以应用到很多领域。风险资本家经常冒险,因为他们有机会进行多项投资。只要投中了一个独角兽(市值10亿美元以上的公司),不仅可以补偿多次失败的投资,还可以带来很大的利润。