非线性函数可以向下或向上弯曲,可以形成S形,还可以扭结、跳跃和波动。
凸函数
凸函数的斜率是递增的。增长和正反馈是产生凸性。
具有正斜率的凸函数会以递增的值增加,具有负斜率的凸函数就会变得不那么陡峭,也就是说,最初具有较大负斜率的凸函数将逐渐走平。半衰期模型(half-life model)中的方程就是如此,这个模型可以用来刻画分解、折旧和遗忘。
指数增长模型(exponential growth model)
描述的是一个变量的数量(通常是指人口或资源)与它的初始值、增长率和周期数之间的函数关系。
时间t的资源值Vt,其初始值为V0,且以速率R增长,可以写成如下方程:
Vt=V0(1+R)t
这个单方程模型在金融、经济、人口、生态以及技术等领域中都发挥着核心作用。当我们把它应用于金融问题时,这里的变量就是货币。
指数增长模型可以研究人口问题。马尔萨斯(Thomas Malthus)就观察到了人口数量呈指数增长的现象,并在给出的一个模型中指出,如果经济体生产粮食的能力是呈线性增长的,就会出现粮食危机。幸运的是,出生率不久之后就下降了,工业革命的到来也极大地提高了生产率。如果这两件事情都没有发生,那么马尔萨斯的预测应该是正确的。关键是,马尔萨斯忽视了创新的潜力。
72法则(Rule of 72)
如果一个变量在每个周期内以R(增长率小于15%)的百分比增长,那么下面提供了一个很好的近似:

半衰期模型
如果每H周期,剩余数量的一半会衰减,那么在t周期后,剩余的比例为:

半衰期模型的一个新应用是在心理学中。早期的心理学研究表明,人们几乎以接近固定不变的速度忘记信息。人们记忆的半衰期取决于事件的显著性。2016年,电影《聚焦》(Spotlight)获得了奥斯卡最佳影片奖。假设,人们对奥斯卡获奖记忆的半衰期为一年,那么到了2018年,有1/4的人会记住这一事实;但是到了2026年,将只有1/1024的人还会记得这件事情。
凹函数
凹函数的斜率是递减的。具有正斜率的凹函数会呈现收益递减的特点:当我们拥有的东西越来越多的时候,每个额外东西所能带来的价值会越来越少。
比如,对任何事物的消费越多,我们就会越不觉得享受,同时愿意为它付出的代价也就越少。
当我们假设了凹性时,也就隐含地假设了对多样性和风险规避的偏好向。
下图说明了为什么凹性就意味着风险规避。这幅图描绘了3种结果的幸福价值(幸福感):高结果(H)、低结果(L),以及前两种结果的平均值(M)。给定形状向下的曲线,平均结果的幸福感会超过低结果和高结果的平均幸福感。
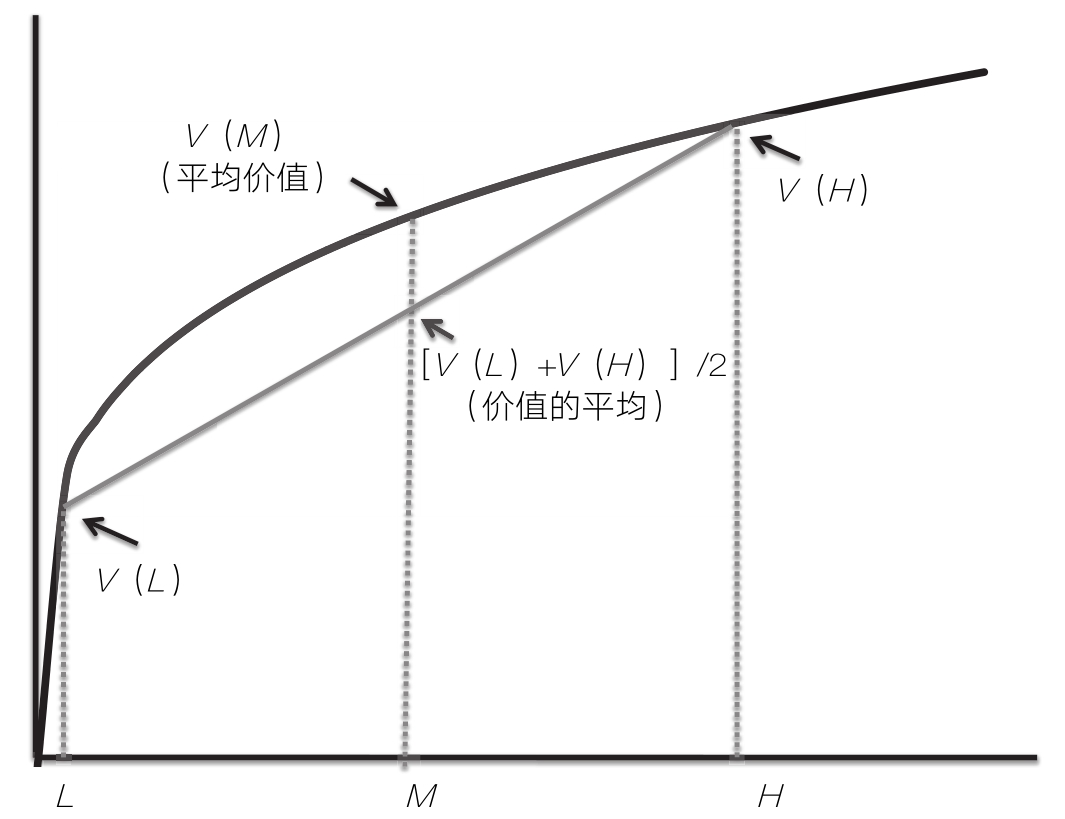
相反,凸性意味着风险爱好:我们更喜欢的是极端值,而不是平均值。可以购买的股票数量是其价格的一个凸函数,因此,股票买家更喜欢价格波动。如果价格不断上涨和下跌,买家最终能够获得的股票比价格保持不变时获得的更多。
经济增长模型
为了给对增长模型的研究奠定基础,我们先引入一个标准的经济生产模型,其中产出取决于劳动和实物资本。经验证据和逻辑都支持产出是劳动力和资本凹函数的假设。保持固定资本,随着投入的劳动力的增加,劳动力的价值应该变得越来越低。同样,在保持工人数量不变的情况下,添加更多的机器或计算机会增加更少的价值。
逻辑推理还表明,产出应该是线性的,工人数量和资本总额翻番应该能使产出翻番。
柯布-道格拉斯模型
给定L个工人和K个单位资本,总产出如下所示:
产出=常数×LaK(1-a)
其中a是介于0到1之间的实数,表示劳动力的相对重要性。
柯布-道格拉斯模型(Cobb-Douglass model)是经济学中使用最广泛的模型之一,它同时包括了两种性质:产出是劳动力和资本的凹函数,而且从规模上看是线性的。这个模型既可以应用于单个企业,也可以应用于行业或整个经济生产。
关键假设是,在柯布-道格拉斯模型中的指数a和(1-a)的总和为1。这个假设意味着如果我们将工人数量和资本数量加倍,总产出也会增加一倍,
我们知道投资是如何推动增长的。现在,我们构建一个包含投资规则的更加精细的模型。
假设工人数量不变。假设投资等于储蓄率乘以产出,并假设机器按某个不变的折旧率折旧。例如,到了年底,不能再用的机器数量等于机器总数的某个固定比例。然后就可以得出,下一年的机器数量等于上一年的机器数量加上新投资的机器数量,再减少因折旧而减少的机器数量。于是,这个完整的简单增长模型由4个方程组成。
简单增长模型
产出函数:O(t) = A x $\sqrt{M(t)}$
投资规则:I(t) = s × O(t)
消费-投资方程:O(t)= C(t) + I(t)
投资-折旧方程:M(t+1)= M(t) + I(t) - d × M(t)
其中,O(t)=产出,M(t)=机器,I(t)=投资,C(t)=消费,s=储蓄率,d=折旧率。
假设这个经济体中有100台机器,储蓄率为20%,折旧率为10%,产量等于1 000吨,消费量等于800吨,新投资200台机器。再假设,因折旧而损失的机器为10台,也就是在新的一年开始时将有290台机器。
第2年,机器:290;产出:1702。投资=(0.2)×1702=340,因此消费=1362。折旧=(0.1)×290=29。
第3年,机器:601,产出:2453。投资=(0.2)×2453=491,因此消费=1962。折旧=(0.1)×601=60。
在第2年,产出将增长为1,702吨,而第3年的产出则将为近2,500吨。由此可见,在这前3年,产出以递增的速度在增长。但是这种凸性只会在前几年出现,原因是机器的初始数量很少,因而折旧几乎完全不会产生任何影响。
在经济的长期均衡中,投资的新机器数量等于折旧损失的机器数量。在这个简单增长模型中,当经济体拥有40,000台机器并生产20,000吨时,这种长期均衡就会出现。在这一点上,经济体在新机器上投入了20%的产出或4,000吨,恰恰等于因折旧而损失的机器数量,也就是40,000台机器当中的10%。因此,因折旧而损失的机器数量等于通过投资和停止增长所创造的新机器数量。
随着时间的推移,机器数量的增加和折旧开始变得十分重要。从长远来看,产出的增长将完全停止。只要分析一下模型,就可以找到原因。投资是线性的,因为增加的新机器的数量是随产出呈线性增加的,同时产出则是机器数量的凹函数。因此,随着经济的增长,投资与机器数量的关系也是凹性的。然而,折旧与机器数量之间却是线性关系。最终线性折旧会赶上产出的凹性增长。
索洛*增长模型
现在构建一个更一般的模型,它是索洛增长模型(Solow Growth Model)的简化,因此我们在索洛后加了一个星号。在完整的索洛增长模型中,会用一个参数a替换掉这里的平方根函数,像在柯布-道格拉斯模型中一样,还包括劳动市场。
我们用实物资本取代机器,并将劳动力视为一个变量。此外,还添加了一个技术参数,它可以线性地增加产出。创新会使这个参数增大。与简单增长模型一样,当投资等于折旧时,长期均衡就会出现。不过,在这里,人们认为均衡时的产出水平取决于劳动力数量和技术参数,以及储蓄率和折旧率。
索洛*增长模型
经济体中的总产出由以下方程给出:
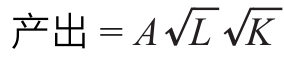
其中,L表示劳动量,K表示实物资本量,A表示技术水平。长期均衡产出O*由下面的方程给出:
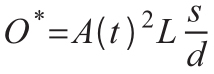
为了求出均衡,我们设定投资等于折旧:
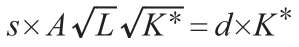
因此,均衡机器数量K*要满足等式:
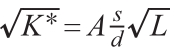
将之代回产出函数,可以求得产出等于:
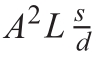
长期均衡产出随劳动力数量的增加、技术的进步、储蓄率的提高而增加,同时随折旧率的上升而下降。
但是,产量随着劳动力数量的增加和储蓄率的提高而线性增长这个事实却着实令人惊讶。劳动只能带来递减的收益,因此如果不考虑模型,我们可能会预测长期产出与劳动力数量之间是凹性关系。但是,随着劳动力数量的增加,产出也会增加,投资也会增加,进而带来更高的产出。从长远来看,投资的正反馈恰好抵消了收益递减。均衡产出与折旧率之间的关系是凸性的,折旧率降低20%可以使产出增加25%。
长期均衡产出也会随技术改进的平方而增加。因此,创新增加的产出要比线性增长更快。如果从一个长期均衡的经济体开始,并将技术参数提高50%,那么产出将会增加50%,投资也将增加50%。然后投资超过了折旧,经济继续增长,投资将继续超过折旧,直到经济再增长50%为止,在这一点上,因折旧而造成的资本损失抵消了投资。这个计算过程揭示了创新乘数(innovation multiplier)的存在,创新有两个效应。首先,创新直接增加产出;其次,创新间接导致更多的资本投资,从而导致产出再次增加。因此,创新是持续增长的关键。
需要注意的是,产出的这些增加不是瞬间发生的。当技术出现了一个突破时,技术参数的变化是相当缓慢的。直接效应的影响需要随着时间的推移显现。旧的实物资本必须被新技术的新实物资本所取代。
当计算机技术进步刚刚发生时,一般企业的计算机不会马上变得更快,只有当技术发生了变化并且企业购买了新计算机之后,它们才会变得更快。
实物资本投资增加导致的二阶增长则会发生在更长的时间范围内。技术与技术对增长的影响之间的滞后,可能意味着创新在出现后的几十年时间内都会导致增长。
火车是在19世纪早期发明的,但是镀金时代(Gilded Age)并没有马上开始,直到19世纪的后半期才到来,这是一个长达50多年的“时滞”。另一个例子是,在阿帕网(ARPANET)出现整整30年后,互联网才开始步入繁盛期。
国家缘何成功与失败
模型证明,资本积累可以实现快速增长,技术投资也可以。一个实物资本较少的落后国家,有可能通过新的资本投入进入技术前沿,从而实现难以置信的高速增长。
创新对长期增长来说是必不可少的,这种必要性也意味着一次性进口新技术有很大的局限性,而持续增长需要创新。
攫取和腐败,也就是政府将经济体的产出挪用于政府开支,会减少储蓄,进而削弱增长。减少攫取和腐败以及促进创新,都能推进经济增长。实现这些目标,需要一个强大但有限的中央政府来促进多元化。强大的中央政府能够保护产权、贯彻法治。多元主义能够阻止精英的俘虏,精英往往更喜欢现状,可能不会接受创新,因为创新往往可能具有很大的破坏性。
增长模型对日本经济增长的解释为实物资本投资的结果。这个模型还预测日本经济增长在一段时间内将会是凹性的。具体来说,这个增长模型的预测是,当日本的国内生产总值接近美国和欧洲时,日本的经济增长率会降低到1%~2%的跨国平均值。证据支持这个预测。从1970年到1990年,日本国内生产总值的年增长率大约为4%。但是从1990年到2017年,它的增长率仅为1%或更低。
皮凯蒂(2014)揭示,从1700年到2012年,世界GDP的年平均增长率仅为1.6%,而且这种增长中的一半是来自人口增长。将72法则应用于这0.8%的年增长率,我们可以发现,在300年的时间内,平均生活水平提高了大约10倍。
非线性的世界
我们看到收益递减和收益递增是许多经济、物理、生物和社会现象的共同特征。最重要的是,我们看到了函数形式能够影响我们的思维,用函数拟合数据有助于做出精确的表述。
科学家可以使用碳-14数据来计算人工制品的年龄,经济学家还可以估计经济小幅增长的长期影响。
一旦包括了非线性,直觉就变得不够用了。直觉可以告诉我们影响的方向:储蓄的增加、劳动力的增加和技术创新可以加快增长。模型还揭示了这些影响的形状和形式。正如我们所料,储蓄具有线性效应。从长远来看,劳动力的增加也是如此,即便模型假设短期收益递减。创新的增加还会产生乘数效应,我们对这种效应取其平方。第一个增长是创新的直接影响,产出的第二次增长则来自资本的增加。