合作博弈
合作博弈由N个博弈参与者和一个价值函数组成。这个价值函数为任何子集S⊆N分配一个值V(S)赋值。这些子集称为联盟。没有博弈参与者组成的联盟的价值等于零。所有N个博弈参与者的价值V(N)等于博弈的总价值。
合作博弈的目标是刻画集体工作和联合项目。在合作博弈模型中,假设人们都会参与,以便我们可以专注于讨论如何为他们的参与分配价值。
最后上车者价值(last-on-the-bus value,LOTB)
在合作博弈中,一个博弈参与者的最后上车者价值等于当他是最后一个加入团队的人时,他所能增加的价值。“最后上车者价值”刻画了边际博弈参与者的价值。
“最后上车者价值”不一定是博弈的总价值相加。特别是,如果价值函数表现出了规模收益递减的性质,那么“最后上车者价值”的总和将小于博弈的总价值;如果增加的价值表现出了规模收益递增的性质,那么“最后上车者价值”的总和将超过博弈的总价值。
如果雇用4个人来搬运一张桌子,假设搬运这张桌子产生的价值为10,并且要4个人一起动手才搬得动,那么每个人的“最后上车者价值”均为10。如果只需要三个人就可以搬动这张桌子,那么每个人的“最后上车者价值”均为零。
夏普利值(Shapley value)
给定合作博弈{N,V},夏普利值的定义如下:
N个博弈参与者加入联盟的次序有N!个,让O代表这所有N!个次序。对于O中的每一个次序,将博弈参与者i增加的价值定义为当博弈参与者i加入时价值函数发生的变化。博弈参与者i的夏普利值等于他在O中所有次序上增加价值的平均值。
考虑一家同时在西班牙和法国运营的小公司,它至少需要一位会讲法语的人和一位会讲西班牙语的人开展日常业务。假设该公司有三名员工:一名会讲西班牙语的人、一名会讲法语的人和一名既会讲法语又会讲西班牙语的双语人士。
现在假设,这个合作博弈为任何一位能讲法语和西班牙语的人分配了1 200美元的价值。如果该公司能够运营,这个金额就等于公司每日的收入。如果任何两名员工来上班了,那么第三名员工就不是必需的。因此,在这个例子中,每个博弈参与者的“最后上车者价值”为零。
为了计算只会讲法语的那个人的夏普利值,我们要考虑这三个人来上班的所有6种可能的次序。在这6种次序中,只有在一种情况下,也就是只会讲西班牙语的人第一个到,然后这个只会讲法语的人第二个到时,这个只会讲法语的人才增加了价值。因此,这个只会讲法语的人的夏普利值就等于1/6乘以1,200美元,即200美元。与此类似,只会讲西班牙语的那个人只有当他第二个到且只会讲法语的那个人第一个到时,才能增加价值,因此他的夏普利值也等于200美元。而在其他四个次序中,既会讲法语又会讲西班牙语的人第一个到或者第二个到都能增加价值,因此,他的夏普利值等于800美元(1200 * 2/3)。所有这三个人的夏普利值总和等于1,200美元,也就是这个博弈的总价值。 </i>
夏普利值的公理基础
零性:如果博弈参与者为任何联盟增加的价值都等于零,那么该博弈参与者的价值等于零。
公平性/对称性:如果两个博弈参与者对任何联盟都具有相同的增加价值,那么这两个博弈参与者具有相同的价值。
完全分配性:博弈参与者价值的总和等于博弈的总价值V(N)。
可加性:给定两个定义在相同博弈参与者集合之上的博弈,它们的价值函数分别为V和$\widehat{V}$,那么在博弈(V+$\widehat{V}$)中,一个博弈参与者的价值等于该博弈参与者在V和$\widehat{V}$的价值的总和。
夏普利-舒比克权力指数(Shapley-Shubik index of power)
夏普利值可以应用于一类投票博弈。在这种投票博弈中,每个博弈参与者(代表某个政党或官员)控制着固定数量的席位或投票权,而且要采取行动,就必须获得多数席位或支持票。在投票博弈中,夏普利值通常被称为夏普利-舒比克权力指数。通过对这个指数的计算,我们发现一个博弈参与者(政党)控制席位(投票权)的百分比与其权力之间并不存在直接的转换。
为了计算权力指数,考虑各个政党加入联盟所有可能的次序。如果某个政党加入了一个联盟并获得绝对多数,那么这个政党所增加的价值等于1。在这种情况下,我们就称这个政党是“关键的”。否则,这个政党不会增加任何价值。
假设议会中共有101个席位,分别由4个政党掌握:A党控制了40个席位、B党控制了39个席位、C党和D党则各控制了11个席位。
在这个例子中,如果A党首先或最后加入,那么A党就不会成为“关键的”政党。但是,如果A党在第二位或第三位加入(各1/4的概率),就肯定会成为“关键的”政党。因此,A党的权力指数为1/2。
如果B党在第一位或最后一位加入,那么它就不能增加任何价值;如果B党在第二位加入,那么当且仅当A党已经在第一位加入时,B党才可能成为“关键的”政党(1/12的概率)。如果B党在第三位加入,那么它要想成为“关键的”政党,唯一的机会是A党在最后一位加入(1/12的概率)。因此,B党的权力指数等于1/6。
C党和D党也可以在两个与B党类似的事件组合中成为“关键的”政党。如果C党或D党在第一位加入,那么不可能成为“关键的”政党。如果A党在第一位加入,那么只要C党或D党在第二位加入(1/12的概率),就能成为“关键的”政党。如果A党在最后一位加入,那么只要C党或D党在第三位加入(1/12的概率),也能成为“关键的”政党。因此,C党和D党的权力指数也分别为1/6。
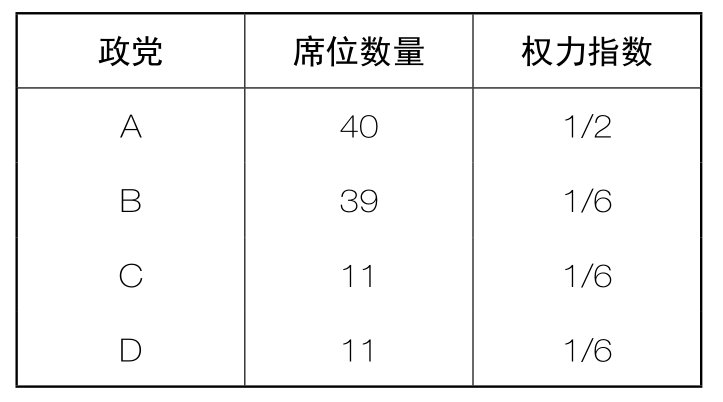
这个例子表明,一个政党控制的席位百分比与它实际拥有的权力之间可能存在着脱节。A党和B党控制的席位数量几乎相同,但是A党的权力却是B党的三倍;B党控制的席位虽然比C党或D党多得多,但是所拥有的权力却不比它们大。 </i>
一些补充
个体的夏普利值与为联盟增加的平均贡献相对应。它是衡量增加价值的一种标准。在投票博弈中,也可以将夏普利值解释为权力的一种度量。不过,夏普利值可能并不一定总是最好的衡量标准。假设威胁是可信的,那么在一个群体已经形成的情况下,个人的“最后上车者价值”可能是衡量权力的一个更好标准,因为它能够度量每个人通过威胁离开可以攫取多大利益。
在这些情况下,联盟会希望减少“最后上车者价值”。通过扩大联盟规模,可以创建出一个具有很高的总价值、同时“最后上车者价值”又足够低的联盟。不断加入新成员,会使现有成员变成“可以放弃的”,从而使“最后上车者价值”趋向于零。
例如,雇主会通过雇用多余的工人来削弱工人的权力,制造业企业会向多个相互竞争的供应商采购中间产品,政府会与多个承包商签订合同,等等。
只拥有微弱多数的政党可能是非常难以驾驭的,因为每一个成员都拥有很大的“最后上车者价值”。而在某个政党拥有了绝大多数席位(投票权)的时候,没有任何众议员或参议员能够拥有太大的权力。 </i>
将视野放大到现代互联网世界,无论是个人、组织、企业,还是政府,抑或是恐怖组织的权力,都部分取决于偏离合作制度可以造成的损害的程度,也就是“最后上车者价值”。一个技术高超的计算机黑客,由于拥有摧毁大量财富的力量,因而拥有巨大的权力。即便黑客完全不能给社会创造价值,这个结论依然成立。