网络的结构
网络由节点以及连接节点的边(edge)组成。由边连接起来的节点互为邻居。如果沿着边,可以从任何一个节点到达任何其他节点,就将这样的网络称为连接的网络。
网络可以用图形来表示,也可以用边的列表表示,或者也可以用由0和1组成的矩阵表示,其中第A行、第B列的一个数字表示节点A和节点B之间的边。
网络中的边可以是定向的,也可以是非定向的。在非定向网络中,一个节点的度(degree)等于连接到它的边的数量。根据中心极限定理,我们知道度是正态分布的,并且其均值为2E/N (N个节点,E条边),因为每个边连接两个节点。
网络以一组网络统计数据为特征。对于每个统计量,我们可以计算网络平均值和所有节点的分布。度分布(degree distribution)告诉我们某些节点是否比其他节点连接得更多。
路径长度,指两个节点之间的最小距离,与度成反比。当增加边时,就缩短了节点之间的平均距离。平均路径长度也与信息丢失相关。经过多人中转传递的信息比直接在两个人之间传递的信息更容易遭到扭曲。
最短路径上的节点在网络中起着关键作用。如果信息是通过最短路径传递的,那么就必定会经过最短路径上的节点。节点的介数得分(betweenness score)等于通过该节点的最小路径的百分比。在社交网络中,介数得分高的人掌握更多信息并且拥有更多权力。
聚类系数,等于节点的邻居节点对当中,同时彼此也互为邻居节点对所占的比例。例如,一个人有10个朋友,这些朋友可以组成45个对。如果在这45个对当中,有15个对本身也是朋友,那么这个人的聚类系数就等于1/3。如果所有这45对都是朋友,那么这个人的聚类系数就等于1,这也是所有可能值当中最大的一个。整个网络的聚类系数等于各个节点聚类系数的平均值。
网络统计量
度:节点的邻居数(即边数)。
路径长度:从一个节点到另一个节点必须遍历的最小边数。
介数:经过某个节点连接两个其他节点的最短路径数量。
聚类系数:一个节点的邻居对当中,同样也由一条边连接的邻居对所占的百分比。
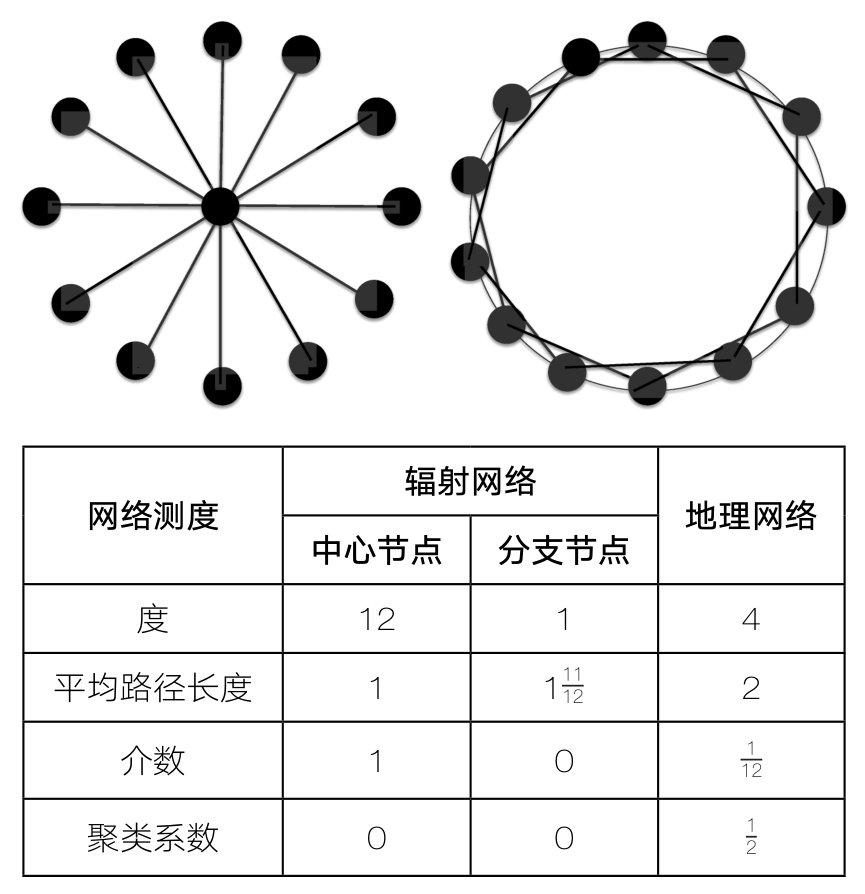
上图显示了一个辐射网络和一个地理网络,它们各具有13个节点。在这个辐射网络中,中心节点的度为12,所有其他节点的度均为1,因此平均度小于2。这种度分布是“不平等”的。中心节点与其他每个节点的距离均为1。所有其他节点与中心节点的距离为1,与中心节点之外的任何一个节点的距离为2。因此,这个辐射网络的平均路径长度也小于2。中心节点位于任何两个其他节点之间的最小路径上,于是介数得分为1。任何一个分支节点都不位于连接其他节点的任何最小路径上,因此它们的介数得分均为0。最后,在这个辐射网络中,连接到某个节点的任何节点都不彼此连接。因此,网络的聚类系数为0。
在这个地理网络中,每个节点都连接到位于它右侧和左侧的两个节点,因此平均度等于4。每个节点到4个节点的距离为1、2、3,因此平均距离恰好等于2。这个地理网络的度和距离分布都是简并性(degenerate)的,因为每个节点都具有相同的度和相同的平均距离。可以看出,每个节点的介数都等于1/12。(给定任何一个节点,它的最小路径长度可以为1到4个节点,也可以为2到4个节点,还可以为3到4个节点,由此,从每个节点开始的最小路径共有12个节点。平均而言,节点的最小路径是访问另一个节点。由此可以得出,每个节点的平均介数等于1/12。根据对称性,所有节点必定都具有相同的介数。)每个节点都有4个邻居,可以构成6个对。在这6个对中,恰好有3对是相互连接的:直接靠着该节点的左右两个节点分别连接到再外一点的节点,并相互连接。因此,聚类系数等于1/2。 </i>
刻画网络的聚集程度的另一种方法是将节点划分为不同的社区(community)。
可以用来确定社区的方法有很多,其中一种方法是依次移除具有最高介数的边,因为介数高的边更有可能将不同的聚类连接起来。还有一种方法是将社区的数量视为给定的,并在特定的目标函数下寻找最佳划分方法,例如最小化社区之间边的数量或最大化社区内部边的比例。
常见的网络结构
少数几个网络统计量无法确定具体的网络结构。我们可以将网络的统计数据与具有相同数量的节点和边的随机网络进行比较,以检验这个网络是不是随机的。
随机网络的蒙特·卡罗方法
为了检验一个具有N个节点和E条边的网络是不是随机网络,可以创建大量具有N个节点和E条边的随机网络,并计算出度、路径长度、聚类系数和介数的分布。然后,执行标准的统计检验,以确定接受还是拒绝那个网络的统计数据可能抽取自该模拟分布的假设。
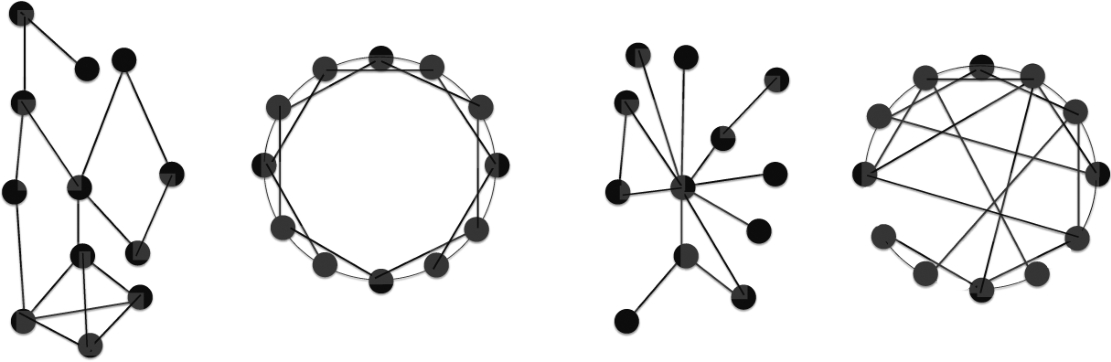
理论模型通常假设某种特定的网络结构。有的研究者偏好假设随机网络,而有的研究者则偏好假设规则的地理网络。
还有一种常见的网络是幂律网络,这种网络的度分布是幂律的。少数节点有许多连接,同时大多数节点的连接则非常少。
第四种常见的网络是小世界网络,它结合了地理网络和随机网络的特征。要想构建一个小世界网络,可以从一个地理网络开始,然后进行“重新布线”,方法是随机地选择一条边并把这条边所连接的其中一个节点替换为一个随机的节点。如果“重新布线”的概率等于零,所拥有的就是一个地理网络;如果“重新布线”的概率等于1,那么就有了一个随机网络;而当概率介于这两者之间时,就会得到一个小世界网络,以小集群区别于通过随机链接连接到其他集群的地理网络。社交网络看起来类似于小世界,每个人都有一群朋友,以及若干随机的朋友。
网络形成的逻辑
我们遇到的大多数网络结构都是从个体行为者做出的关于建立连接的选择中涌现出来的。友谊网络、万维网和电网都是如此。这些网络不是计划的结果。不过,也有一些网络,例如供应链网络,确实是计划的产物。我们希望按计划构造的网络对节点的故障具有鲁棒性。当然,自发涌现的网络结构都具有鲁棒性。
网络的功能
友谊悖论
如果网络中任何两个节点的度不同,那么平均而言,节点的度会低于其相邻节点。换句话说,平均而言,人们的朋友比他们自己更受欢迎。
事实上,在任何网络上,平均来说,人们确实不可能比他们的朋友拥有更多的朋友。我们可以利用辐射网络来说明出现这种情况的原因及其背后的逻辑。在辐射网络中,12个人中的每人都只有1个朋友,只有1个人有12个朋友。有1个朋友的那12个人都连接到了中心节点,中心节点有12个朋友。这个特征,也就是度更高的人与更多的人连接在一起的事实,驱动了结果。在中心网络上,平均来说,所有人只有不到两个朋友。然而,平均而言,每个人的朋友都有超过11个朋友。
平均而言,一篇学术论文引用的参考文献被引用的次数比这篇文章本身更多;与一个国家的贸易伙伴进行贸易的国家数量,要比与这个国家进行贸易的国家更多;食物网络中与单一物种相连接的多个物种的连接比该物种自身更多。在具有更加分散的度分布的网络上,朋友的数量与朋友的朋友的数量之间的差异会变得更加明显。例如,根据Facebook的数据对友谊网络进行的一项研究结果表明,一个人平均大约有200个朋友,而他们的朋友平均来说有超过600个朋友。
六度分隔理论,也就是地球上的任何两个人都可以通过6个或更少的朋友联系到一起。虽然友谊悖论适用于任何网络,但是六度分隔却只适用于某些类型的网络。
我们构建了一个简化版的小世界网络,以便直观地理解六度分隔理论。这个小世界网络假设每个人都有一个由若干个圈内好友构成的小群体,这些人彼此认识,而且每个人都拥有不属于这些圈内的朋友,我们把这些圈子外的朋友称为“随机朋友”(random friends)。下图表明,某人(用黑色圆圈表示)有5个圈内好友和两个随机朋友。它还显示了这个节点的朋友(用浅灰色圆圈表示)的部分“朋友圈”。
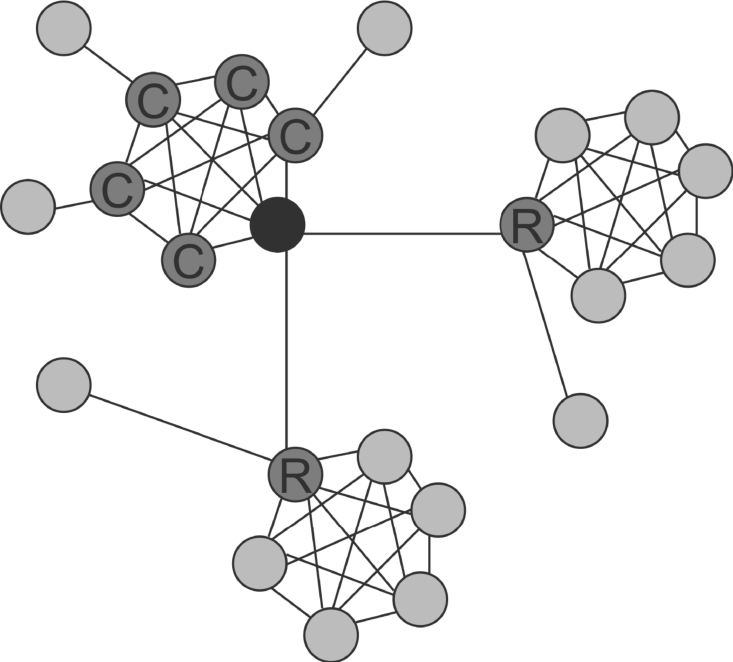
这些随机朋友也可以认为是一种弱关系,他们可以将你连接到其他群体的人。我们的弱关系,也就是网络中的随机朋友,由于连接了具有不同兴趣和信息的社区,从而发挥了重要的信息作用。因此,社会学家很强调弱关系的力量。
在这种网络结构中,我们可以计算出二度邻居,也就是朋友的朋友的数量,方法是将随机朋友的所有朋友人数相加,但是不把圈内好友计算在内,因为他们本身就是节点群体的成员。与此类似,我们可以计算出朋友的朋友的朋友的数量,方法是把所有“圈内好友”的随机朋友的朋友加进来,但是不把随机朋友的“圈内好友”的“圈内好友”计算在内,因为他们在计算二度邻居时已经加进来了。为了产生六度分隔,我们将相同的逻辑应用于一个具有100个“圈内好友”和20个随机朋友的网络。
六度分隔
假设每个节点有100个“圈内好友”(C),他们彼此都是朋友;以及20个随机朋友(R),他们没有与节点共同的朋友。
一度:C+R=120
二度:CR+RC+RR=2 000+2 000+400=4 400
三度:CRC+CRR+RCR+RRC+RRR=328 000
四度13:17 360 000 (四度朋友的数量是通过对如下8组节点求和来计算的:CRCR=4 000 000,CRRC=4 000 000,RCRC=4 000 000,CRRR=800 000,RCRR=800 000,RRCR=800 000,RRRC=800 000,RRRR=160 000)
五度:>10亿
六度:>200亿
由于假设随机朋友的朋友之间没有重叠,这个模型隐含地假定人口是无限的。但是在现实世界中,随着度数的增大,真实的社交网络会出现朋友之间的重叠。在包括了重叠和其他真实世界特征(例如朋友数量的异质性)的网络中,实际值将会与上面计算出来的值不同。不过,每个度的邻居数量的相对大小将保持相似:一个人的三度邻居(朋友的朋友的朋友)会比二度邻居(朋友的朋友)多得多。
三度朋友可能是相当重要的,他们会更加多样性。他们也足够接近,可以建立起信任关系。三度朋友的数量很重要,他们的多样性以及相对接近性使他们成了你的重要资产,他们可以提供新的信息和工作机会。这些人最有可能帮助你找到工作,促使你搬到新的城市,或者成为生活中、商业上的伙伴。
网络结构的鲁棒性
网络最重要的性质是,它在受到冲击时是不是仍然能保持连接。我们可以使用模型来计算网络保持连接的概率——作为移除节点数量的函数。还可以考察当移除某些节点时平均路径长度会发生什么变化。
缺乏局部聚类的稀疏网络更容易出现故障。在电网中,节点或连接如果发生了故障,是不能通过聚类中的其他连接或与仍然有效节点的远距离连接来克服的。因此,局部故障就级联放大地传播到整个网络。与此形成鲜明对照的是互联网。具有长尾度分布的互联网对随机节点故障具有很强的鲁棒性。互联网的度分布意味着,绝大多数节点的连接很少,因此即便它们发生了故障,网络也能保持连接。
战略性地移除度最高的节点会破坏整个网络。可以从辐射网络看出其逻辑。当随机移除节点时,辐射网络仍然可以保持连接,除非直接移除中心节点,但那是一个低概率事件。然而,战略性地移除节点,即直接毁灭中心节点,却可以一步切断网络连接。
例如恐怖主义网络和毒品贸易网络是我们想要切断的。如果这些网络是像电网那样的稀疏网络或者具有长尾度分布,那么就可以通过移除战略节点来断开这些网络。对于恐怖主义网络来说,这意味着必须逮捕拥有链接最多的恐怖组织成员。如果这些网络类似于小世界网络,那么它们就会具有鲁棒性,甚至在战略性的节点被移除之后仍然能屹立不倒。尝试切断这种网络任何“区段”的努力都将失败,因为随机重新连接的存在会将这些“区段”重新连接到网络上。
小结
在社会网络中,一个人的成功、行为、信息或信念,会影响他们的朋友的成功、行为、信息或信念。一个人的价值或贡献可能是源于他本身的某种性质,但是,一个人的成功或许也可以归功于其朋友和同事的网络。
恰恰是那些在网络中占据了最核心位置的人做出了最大的贡献。在网络中占据了介数很高位置的那些人,填补了社区之间的“结构洞”(structural holes)。当然,要想去填补结构洞,得有相当高的才华和能力。看到一个洞就跳下去并不算填补结构洞。要填补结构洞,你必须让社区的每一个人信任和理解你,你必须熟悉每个社区的知识库。
我们还可以对企业的价值进行评估并讨论国家的权力分配。我们可以将企业的价值视为内在价值,着重从资产负债的角度分析。还可以考察该企业运营的情境,例如它在供应链中的位置。与此类似,一个国家的权力取决于它的资源和联盟。