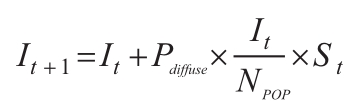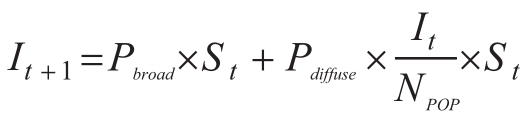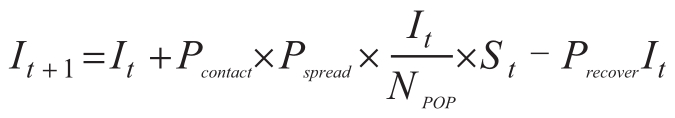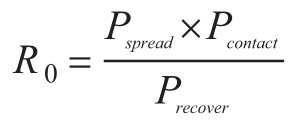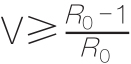广播模型
假设存在一个相关人群,用NPOP表示。相关人群包括那些可能患上传染病、了解信息或采取行动的人。在任何时候,总会有些人患上了某种传染病、了解特定信息或采取了一定行动。我们将这些人称为感染者或知情者(用It表示),相关人群中除了感染者或知情者之外的其余成员则是易感者(用St表示)。相关人群的总人数等于感染者或知情者人数加上易感者人数的总和:
NPOP = It + St
It+1= It + Pbroad × St
其中,Pbroad表示广播概率,It和St分别等于时间t上的感染者(知情者)和易感者的数字
初始状态为I0 = 0,且S0 = NPOP。
这些模型都假设了离散的时间(步长),例如,天或周,并使用差分方程来描述“明天”被感染(或变得知情)的人的数量与“今天”被感染(或变得知情)的人的数量之间关系。连续时间模型则需要运用微分方程和微积分。但是,如果改用连续时间模型,那么结果从定性的角度来看不会有所不同。
这个模型的目标是描述一个信息源传播信息的过程,可以是政府、企业或报纸。它也适用于通过供水系统传播污染的情况。但是,这个模型不适用于在人与人之间传播的传染病或思想。由于广播模型更适合描述思想和信息的传播(而不是传染病的传播),所以我们在这里说知情者的人数,而不说感染者的人数。
按照惯例,初始人口全部由易感者组成。要计算未来某期的知情者人数,只需要将知情者人数和易感者人数代入上述方程即可。由此得到的将是一个r形采用曲线。
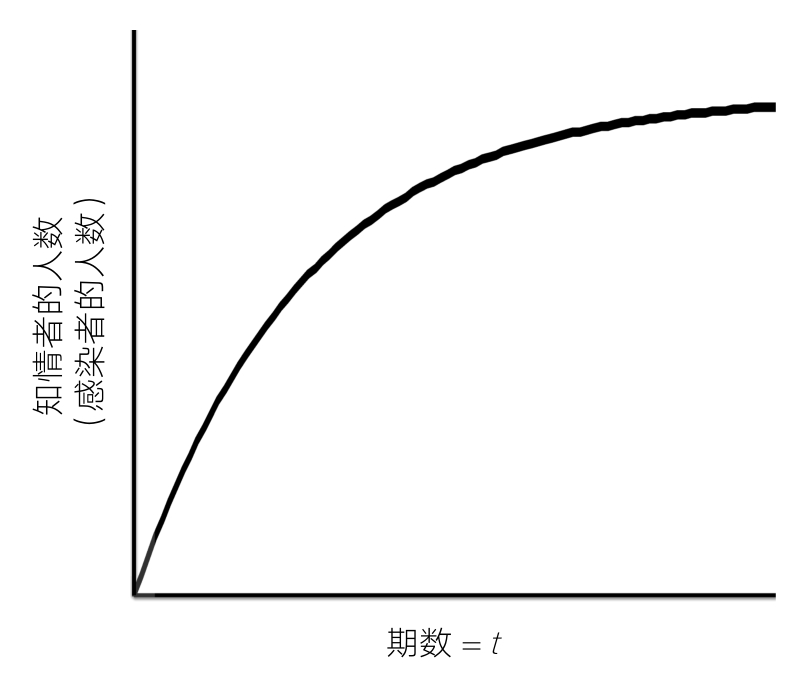
相关人群中的每一个人最终都会知悉信息。如果有适当的数据,就可以估计出相关人群的规模。
假设一家企业为练习太极拳的人推出了新设计的运动鞋,并在第一个星期就收到了20,000双鞋的订单。如果在第二个星期收到了16,000双鞋的订单,那么我们可以大致估计出他们最终的总销售量,也就是相关人群的规模为100,000。
用广播模型拟合销售数据
第1期:I1 = 20,000 = Pbroad × NPOP;
第2期:I2 = 36,000=20,000 + Pbroad ×(NPOP - 20,000)
于是,总销售量为:Pbroad = 0.2,NPOP = 100,000
这个模型无疑遗漏了许多现实世界的特征。人们既可能通过传媒获悉相关消息,也可能通过口耳相传听到消息,而且有些人可能会购买不止一双鞋子,或者可能存在针对潜在消费者的广告,等等。如果把这些因素都包括进去,估计出来的结果肯定会有所不同。 </i>
扩散模型
大多数传染病,以及关于产品、思想和技术突破的信息,都是通过口口相传而传播开来的,扩散模型刻画了这些过程。扩散模型假设,当一个人采用了某种技术或患上了某种传染病时,这个人有可能将之传递或传染给与他接触的人。
在传染传染病的情况下,个人的选择不会在其中发挥任何作用。技术的传播则与采用者的选择有关,因此更有用的技术被采用的概率更高。但是在这里,我们并没有在模型中明确将这种情况选择考虑在内。
我们将人们分为知情者或不知情的新人。如果新人与知情者相遇且信息在他们之间传播,那么新人就会变成知情者。我们将扩散概率(diffusion probability)定义为接触概率(contact probability)和分享概率(sharing probability)的乘积。我们可以根据扩散概率来构建模型,但是在估计或应用模型时,必须独立地跟踪接触概率和分享概率。
扩散模型假定随机混合(random mixing)。随机混合的含义是,相关群体中任何两个人接触的可能性都相同。如果将它应用于城市人口则是有问题的。在城市中,人们并不是随机混合的。但是,一个假设要成为有用模型的一部分,其实不一定非得十分准确不可。
其中,Pdiffuse = Pspread × Pcontact
在这个模型中,与在传播模型中一样,从长期来看,相关人群中的每个人都会掌握信息。不同的是,扩散模型的采用曲线是S形的。
最初,几乎没有人知情,I0很小。因此,能够与知情者接触的易感者人数也必定很小。随着知情者人数的增加,知情者与不知情者之间接触的机会增加,这又使知情者的人数更快地增多。当相关人群中几乎每个人都成了知情者时,新知情的人数会减少,从而形成了S形的顶部。
利用扩散模型的数据估计相关群体的规模可能会非常困难。产品销售量的增加,可能是由于一个很小的相关人群内部的高扩散概率,也可能是由于一个很大的相关人群中的低扩散概率。
在使用扩散模型来指导行动的时候,我们必须将扩散概率分解为分享概率和接触概率的乘积。为了提高应用程序的销售速度,开发人员既可以设法提高人们相互接触的概率,也可以设法加大他们分享关于应用程序信息的概率。要想改变第一个概率是很困难的。为了增大第二个概率,开发人员可以为带来了新注册用户的老用户提供一些激励。虽然这样做能够增加扩散速度,但是并不会影响总销量,至少根据这个模型来看不会有影响。如上所述,总销量等于相关人群的规模,而与分享概率高低无关,提高销售速度不会带来长期的影响。
巴斯模型
大多数消费品和信息都是通过广播和扩散传播的。而巴斯模型则将这两个过程组合在一起了。巴斯模型中的差分方程等于广播模型和扩散模型中的差分方程之和。在巴斯模型中,扩散概率越大,采用曲线的S形就越显著。电视、收音机、汽车、电子计算机、电话机和手机的采用曲线形状都是r形和S形的组合。
其中,Pbroad = 广播概率,Pdiffuse = 扩散概率
SIR 模型
我们将放弃所采用的某种事物的人称为痊愈者。由此产生的模型,即SIR模型(易感者、感染者、痊愈者),在流行病学中占据了中心位置。
为了避免过于复杂的数学计算,我们假设治愈传染病的人会重新进入易感人群,也就是说治愈传染病并不会产生未来对传染病的免疫力。
其中,Precover,Pspread,和Precover分别等于传染病的传播概率、接触概率和痊愈概率。
基本再生数R0
SIR模型会产生一个临界点,就是所谓的基本再生数R0,也就是接触概率乘以扩散概率与痊愈概率之比。某种传染病,如果R0大于1,那么这种传染病就可以传遍整个人群,而R0小于1的传染病则趋于消失。在这个模型中,信息(或者,在这个例子中是传染病)并不一定会传播到整个相关人群。能不能做到这一点取决于R0的值。
如果存在疫苗,那么疫苗接种可以预防传染病传播。即便做不到每个人都接种疫苗,也可以预防传染病传播。必须接种疫苗的人的比例,即疫苗接种阈值(vaccination threshold),可以通过公式求出。
疫苗接种阈值随R0的增加而提高。例如,脊髓灰质炎的R0为6,因此为了防止脊髓灰质炎的传播,疫苗必须覆盖5/6的人群。
如果不接种疫苗的人只占人口的一小部分,那么其他人接种疫苗也可以防止这些人感染这种传染病,流行病学家将这种现象称为群体免疫力。
超级传播者,以及度的平方
如果将SIR模型嵌入到网络中,就会观察到度分布对传染病传播的重要性。
对于中心辐射型网络,如果中心节点患上了传染病,传染病就会传播开来。流行病学家们将位置在度很高的中心节点上的人称为“超级传播者”(superspreaders)。超级传播者不一定是社交明星或“人脉”特别广的人,可能从事某种特定的行业职业,比如收费站的收费员、银行柜员、牙科医生,这类职业使他会与属于不同社交网络的人接触。
高度数节点不但能够更快地传播传染病,而且会更快地患上传染病。节点对传染病(或思想)传播的贡献与节点的度的平方相关。如果节点A的度数是节点B的K倍,那么节点A传播传染病的可能性是节点B的K倍,同时传染病传播到节点A的概率也是节点B的K倍。因此,节点A对传染病传播的总效应将是节点B的K2倍。这种现象被称为度的平方。
一对多
在SIR模型中的两个关键阈值,R0和疫苗接种阈值,都是属于敏感依赖于环境的临界点,环境(情境)中的微小变化都会对结果产生很大的影响。
在将广播模型、扩散模型和传染模型应用于社会现象时,我们可能会发现某些假设是成立的,而其他一些假设则不能成立。例如,在某种传染病的传播中,每一次接触导致该传染病传播的概率是独立的。但是在社交领域,由于采用本身也是一种选择,因此传染有可能会因更多的接触(曝光)而变得更有可能。流感不是我们选择的,我们只是得了流感。但是我们会选择买紧身牛仔裤,随着越来越多的人穿上了紧身牛仔裤,我们所有人都更可能穿紧身牛仔裤。在这些情况下,我们可能必须对基本模型进行修正,以允许每次接触的采用概率会随着接触次数的增多而增大。