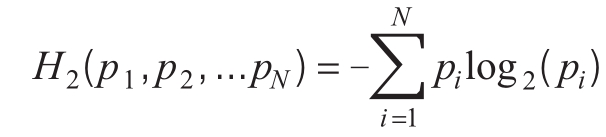熵是对不确定性的一个正式测度。
在没有控制或调节力量的情况下,一些群体可能会向最大熵漂移。给定特定的约束条件,例如不变的均值或方差,就可以解出最大熵分布。最大熵分布的结果还可以用来证明某些分布比其他分布更优,从而能够对我们在建模时的选择起到指导作用。
熵与方差不同,方差度量一个数值集合或数值分布的离散程度。不确定性与离散程度有关,但是两者并不是一回事。
信息熵
给定一个概率分布(p1,p2,…, pN),信息熵,H2等于:
熵的公理基础
-
连续的
-
对称的
-
在所有结果以相同的概率发生时最大化,同时在某些结果上等于零。
-
在具有m个子类别的n个类别上定义的概率分布的熵,等于各类别上的分布的熵与每个子类别的熵的总和。例如,在结果是两个独立事件的乘积的情况下,这意味着联合事件的信息内容是每个事件单独发生时的信息内容的总和。
利用熵区分结果类别
对经验数据可以分成四大类别:均衡、周期性、随机性和复杂性。
放在桌子上的铅笔处于均衡状态,绕太阳运转的行星处于循环当中,抛硬币的结果序列是随机的,纽约证券交易所的股票价格也是近似随机的。最后,一个人大脑中的神经元发放则是复杂的:它们既不会随意发放,也不会以某个固定的模式发放。
平衡结果没有不确定性,因此其熵等于零。周期性过程具有不随时间变化的低熵。完全随机过程具有最大的熵。复杂性具有中等程度的熵,因为复杂性位于有序性和随机性之间。
为了对时间序列数据进行分类,我们需要先计算出不同长度的子序列中的信息熵。假设,有个人会把他每天戴的帽子的类型一一记录下来。假设他只在两种帽子之间进行选择。这样过了一年,他对帽子的选择生成了一个有365个事件的时间序列。我们先计算长度为1的子序列的熵,也就是说,先计算戴每种类型帽子的概率的熵。假设他喜欢这两种类型的帽子的程度相同,那么长度为1的子序列的熵等于1。因此,我们可以先把均衡排除掉,因为他会改变他的选择,但是其他三种类别中的任何一种都是可能的。
为了确定类别,我们接下来计算长度为2到6的子序列的熵。如果所有都具有最大的熵,那么我们可以将简单的周期性排除掉。假设当我们考虑更长的序列时,熵会缓慢增加,直到达到最大值8为止。换句话说,无论子序列有多长,熵都不会超过8。熵为8相当于256个结果的等可能分布,这不可能是一个简单的循环。熵为8更可能代表具有特定结构和模式的复杂过程序列。我们不能确定地说,这个时间序列是复杂的。一种可能的情况是,这个人试图做到随机化,但是却失败了。 </i>
最大熵和分布假设
我们建模时都必须把不确定性包括进来;必须对有关的分布做出假设。这里的原则是,我们要尽量避免做出任意特殊假设。如果我们对产生分布的过程已经有了一些了解,那么通常可以运用逻辑—结构—功能方法,推导出该过程产生的统计结构。
最大熵分布的形状取决于各种约束条件。
-
如果假设了一个最小值和一个最大值,那么均匀分布会使熵最大化。许多社会科学模型都假设均匀分布,虽然均匀分布在现实世界中确实很少出现。但是无差别原则可以证明假设均匀分布的合理性。如果只知道范围或可能集,那么就应当予以无差别的对待。
-
如果可能知道分布的均值,也知道所有值都必定是正数。给定这些约束条件,最大熵分布必定具有长尾,因为我们要将分布置于更多的值上,从而必须使少数高值结果与许多低值结果保持平衡。熵最大化分布是一个指数分布。因此,如果我们正在构建一个模型,需要假设网站点击量或市场份额的分布形式,那么在没有可用数据的情况下,指数分布是一种自然的假设。
-
如果确定了均值和方差(并且允许出现负值),那么最大熵分布则是正态分布。为了创造更多的不确定性,我们创造了一些极端值,在这里,可以平衡正值和负值,而不用改变均值。但是,这样做会增大方差,因此我们必须在均值附近添加更多值,从而创造出钟形曲线。
如果我们认为在给定的社会、生物或物理环境中,某个微观层面的过程能够最大化熵,那么我们应该期待上面这些分布中的某一个会出现。或者也可以假设一个微观过程,并能够证明熵在增加。如果是这样,上述分布中的某一个也会涌现出来。
我们利用中心极限定理解释了物种的高度、重量和长度为什么会服从正态分布。在这里,我们再给出一个不同的、基于模型的解释:如果一种突变能够最大化熵(以便探索最好的生态位),并且假设平均规模和总离散度是固定的,那么规模的分布将会是正态的。关键不在于这种最大熵方法是不是提供了一个更好的解释,而在于给定约束下最大化熵必定会导致正态分布。因此,当我们看到正态分布时,它可能是最大化熵的结果。
熵的实证含义和规范含义
我们可以将熵测度用于任何实际应用,可以用它来衡量对金融市场的干预是增加了还是减少了不确定性,可以检验选举、体育赛事或博彩中的结果到底是不是随机的。
在这些应用中,熵都是作为一个实证的衡量标准来使用的。它告诉我们世界是什么样的,而不是世界应该是什么样。一个系统中的熵的本质,不能简单地说好,也不能简单地说不好。我们想要多少熵,取决于具体情况。在制定税法时,我们可能需要一种均衡行为模型,并不希望有随机性。在规划城市时,我们可能会希望看到复杂性,均衡或者周期性都会显得过于平淡。我们希望一个城市充满生机活力,为偶然的相遇和互动提供无限机会。在这种情况下,更多的熵会更好,但是又不能太多。我们不喜欢随机性,随机性会使计划变得非常困难,并可能导致我们的认知能力崩溃。最理想的情况是,世界会产生适度的复杂性,以保证我们生活在一个有趣的时代。