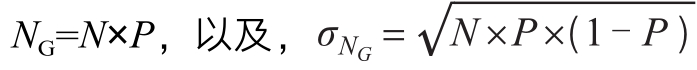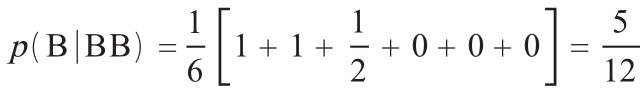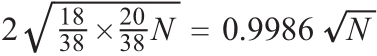伯努利瓮模型(Bernoulli urn model)
伯努利瓮模型由一个装了灰球和白球的瓮组成。从瓮中抽取的球代表随机事件的结果。每次抽取都与之前和之后的抽取无关,因此我们可以应用大数定律:从长远来看,抽出每种颜色的球的比例将会收敛到这个球在瓮中的比例。
大数定律说明平均比例是收敛的,而中心极限定理则告诉我们白球比例的分布是正态的。
每一次,从一个装了G个灰球和W个白球的瓮中随机抽取一个球,结果等于抽取出来的球的颜色。在下一次抽取之前,球要先放回瓮中。令P = G/(G+W)表示灰球的比例。在抽取N次的情况下,可以计算出抽取出来的灰球的期望数量NG,及其标准差:
在灰球和白球数量相等的瓮中,抽取出白球的概率等于1/2,连续抽取出两个白球的概率等于1/2乘以1/2,以此类推。一般情况下,如果瓮中白球的比例为P,那么连续抽取N个白球的概率等于PN。通过计算概率,我们可以评估某种运气是不是有可能出现(尽管很令人吃惊),或是几乎完全不可能(因而基本上可以肯定“有诈”)。
一位三分球命中率为46%的篮球运动员连续投中9个三分球的概率大约为1/1 000(0.469)。如果这个篮球运动员一直继续投三分,那么在10年的NBA生涯中(总共参加大约800场比赛),一次都做不到三分球9投9中的概率大约为47%(0.999800)。
任何一次投篮或罚球命中的概率是否与前一次的成功相关?在考虑“热手效应”的证据时,我们必须考虑到行为。如果一名篮球运动员认为自己的手感很好,那么可能会尝试更加困难的投篮。此外,如果防守方觉得对方哪个运动员手感太好,他们就会收紧对他的防守。这些行为反应在模型中可以通过加大难度来体现。有一些研究收集了多名(例如)篮球运动员投篮命中和不中的序列;然后再计算随机选择的多次投篮后某次投篮命中的概率。这种采样程序会引入一种微妙的统计偏差。
为了说明这种偏差,不妨考虑如下这种情况:多名篮球运动员每人只投篮4次,而且每次投篮都有相同的命中概率,这样就有16种可能的投篮命中和未命中的序列。我们用B代表投篮命中,用M代表投篮不中。在这16个序列中,有6个是连续两次命中后再接着投篮一次产生的,它们是:BBBB,BBBM,MBBB,BBMB,BBMM和MBBM。这些都是连续两次投篮命中后再投第三次篮的情形。如果抽到了BBBB,那么无论选择哪一个由两个B组成的序列,那么接下来再投篮命中的概率都等于100%。如果选择了MBBB,那么B跟着BB出现的概率也等于100%。但是,如果选择了BBBM,那么BB之后出现M的概率等于50%。最后,如果选择的是MBBM、BBMB或BBMM,那么M必定会在BB之后出现。求这6种情况的平均值:
之所以会产生偏差,是因为在序列BBBB中,有两个BB可以选择,但是在其他序列中,则只有一个(例如,BBMB)。前述采样程序使得BBBB的这两个子序列中的每一个被选中的概率都仅为BBMB中的那一个子序列的一半。这种偏差的含义是,如果不存在“热手效应”,那么这种采样程序就已经证明投篮命中后再投篮时更有可能不中。当然事实并非如此,而这就意味着投篮命中之后再投篮实际上更有可能命中。 </i>
随机游走模型
随机游走模型建立在伯努利瓮模型的基础上的,保持了正面和反面的总数。这个模型可以刻画液体和气体中粒子的运动,动物在物理空间中的活动,以及从出生到童年人体身高的增长,等等。
将初始值,也就是模型的初始状态设置为零。如果我们抽取出一个白球,就在总数上加1;如果抽取出一个灰球,就从总数中减1。模型在任何时候的状态都等于先前结果的总和,也就是抽取出来的白球总数减去抽取出来的灰球总数的值。
简单随机游走模型
Vt+1=Vt+R(-1,1)
其中,Vt表示时间t上的随机游走值,V0=0,R(-1,1)是一个可能等于-1或1的随机变量。在任何时间段内,这个随机游走的期望值都等于零,且标准差为$\sqrt{t}$,其中的t等于周期数。
一个随机游走的值是相同的、独立的随机变量的总和,我们就可以求解标准差。每个随机变量的均值都为零,而且取值为+1或-1。因此,每个都具有1的标准差。设置σ=1并且对所得到的总和应用西格玛平方根公式,就可以得出标准差。
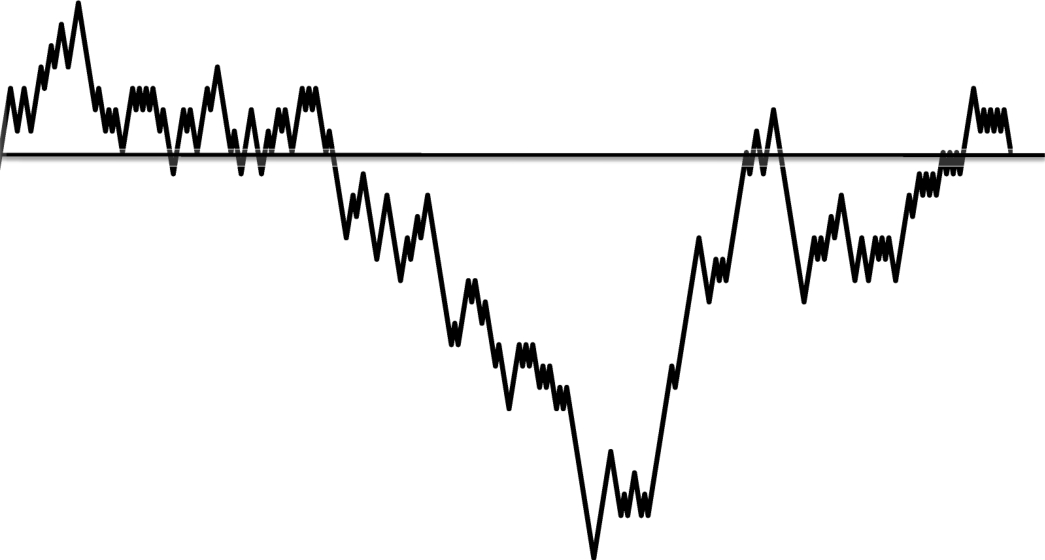
简单随机游走既是周期性的(会无限次地返回零点),又是无界性的(会超过任何正的或负的阈值)。如果等待足够长的时间,随机游走会高于正的1万、低于负的100万,也会无限次地穿过零线。此外,返回零点所需的步数分布满足幂律。在大多数时候,返回零只需几步。所有游走中,有一半是两步返回的,然而有些游走需要很长时间才能返回。鉴于随机游走的无界性,这必定是真的。一个超过100万步阈值的游走,需要超过200万步才能到达那里并返回零点。
一维和二维随机游走会无限次地回到起点,而三维随机游走则可能完全不需要回到起点。
如果我们将企业的销售水平或员工规模建模为随机游走,那么企业的生命周期就会成为一个幂律分布。销售强劲时,企业会新招聘一名员工;当销售不佳时,会解雇一名员工;当不再拥有任何员工时,企业也就“寿终正寝”了。这样一来,返回次数的分布就等于企业生命周期的分布,而且是一个幂律分布。再者,就其第一近似而言,企业的生命周期是一个幂律。我们可以应用相同的逻辑来预测生物分类单元(界,门,经,纲,目,科,属和种)的寿命。如果某个分类单元的成员数量遵循随机游走,例如,如果某个属中的物种数量随机地上下变化,那么,这个分类单元的大小就应该满足幂律。这方面的数据支持了这个模型的预测。
这个基本随机游走模型可以通过多种方式加以修正。我们可以创建一个正态随机游走(normal random walk)。在正态随机游走中,每一周期的值的变化都服从正态分布。正态随机游走不会完全回到零点,但它会无限次地穿过零点。
我们还可以令某一种结果比另一种结果更有可能发生,从而创建一个有偏差的随机游走。我们可以利用这种有偏差的随机游走模型来预测在博彩中获胜的概率。
轮盘赌中,在红色结果上下注时赢的概率等于9/12。我们可以将赌轮盘赌的总收益或总损失建模为这样一个随机游走:增加1的概率为9/19(大约47.4%),而减少1概率则为10/19。
N次投注后,这随机游走的期望值等于N * ($\frac{18}{38}$ - $\frac{20}{38}$) = $\frac{-N}{19}$。由于获胜的概率大约为1/2,我们可以将这个值的标准偏差近似为$\sqrt{N}$。确切的值则等于
在下注100次之后,预期损失为5美元,标准差为10美元。这也就是说,我们可以在95%的置信水平上,认为损失不超过25美元、收益不超过15美元。在下注1万次之后,预期损失等于526美元,标准差为100美元。因此,在95%的置信水平上,我们的损失介于325美元与725美元之间。同样,在下注1万次之后,我们还能赢是一个相当于超过均值5个标准偏差的事件,也就是说我们赢的可能性不到百万分之一。因此,要想在轮盘赌中赢,应该做的事情是下一个大赌注而不是下很多个小赌注。
一些体育比赛,例如篮球比赛,可以建模为两个有偏差的随机游走。在球场上,每支球队在每次攻守中都有可能得分。这个概率可以根据一支球队的进攻能力和对方球队的防守能力来估计。我们将球队在球场上的“行程”模拟为一个随机事件。每支球队的得分对应一个随机游走值。来自NBA的数据分析表明,实际比赛结果与这个模型匹配得相当好。只有当一支球队获得了巨大的领先优势时,得分才会偏离随机性,在那种情况下领先优势继续扩大的可能性低于领先优势缩小的可能性。
模型还提出了一个策略:更强的那支球队应该加快比赛节奏,以创造更多的进攻回合。占有优势的球队应该更频繁地玩“轮盘赌”,因为随机“漂移”对他们有利。 </i>
二维随机游走从平面中的原点(0,0)开始,然后在每个周期中随机走向东、南、西、北。二维随机游走类似于在一张纸上绘制出来的一条弯弯曲曲的线,同时也满足递归性(recurrence)和无界性,有点类似于在你的起居室中随机搜索一只丢失的耳环时的路线。这种递归性使随机觅食成了蚂蚁的一个觅食策略。如果二维随机游走不是递归性的,那么蚂蚁就需要更复杂的内部地图或更强的信息踪迹才能找到它们的巢穴。
在有三个维度的情况下,随机游走将不再满足递归性。在一个房间里到处飞的苍蝇和在空气中弹跳的分子都只会有限次地返回到它们的起点。
直觉告诉我们,当添加维度时,返回起点的次数应该会减少,而逻辑则表明,这里会出现一个突然的变化。在一维和二维的情况下,随机游走会无限次地返回起点。而在三维的情况下,它将“永恒在外游荡”。
使用随机游走估计网络规模
可以利用低维随机游走的递规性来估计某个网络的规模。随机选择一个节点,然后沿着网络的边开始随机游走,并跟踪它回到初始节点的频率。返回到初始节点所需的平均时间与网络的规模相关。例如,为了估计一个社交网络的大小,可以要求某人指定一个朋友,然后让那个朋友再说出一个朋友的名字,一直继续这个过程,看需要多久才会返回到同一个人。
随机游走与有效市场
股票价格接近正态随机游走,带有正漂移,以获得市场收益。许多个股的价格也接近随机。
对Facebook的股价序列进行统计检验,以确定它是不是真的满足正态随机游走的假设。首先,价格应该以相同的概率上下波动,在这个序列所涵盖的249个交易日内,Facebook的股票价格在127天内是下跌的,占总交易日数的51%。其次,在随机游走中,增加的概率应该与前一周期的增加无关,Facebook的股票价格连续两天在同一方向上发生变化的时间只占总时间的54%。最后,持续出现在同一方向上的最长波动应该是8天,在这一年时间里,Facebook的股票价格曾连续10天上涨。因此,总的来说,我们不能否认Facebook的股票价格与正态随机游走一致的假设。
股票价格可能遵循随机游走的原因是,聪明的投资者能够识别出并消除这种模式。经济学家将市场价格的可识别持久模式类比为人行道上的百元钞票。如果有人看到人行道上有张一百元的钞票,就会把它捡起来,然而只要这样做了,钞票就会消失。同样的逻辑适用于股票价格模式:如果它们存在,它们就会消失。因此,充满了聪明的投资者的市场几乎必定不会包含什么可预测的价格模式。既然价格不会呈现出任何模式,那也就只能是随机游走了(需要注意的是,必须先去除一般的上行趋势)。
一些经济学家将这种随机游走思想进行了扩展,提出了有效市场假说(efficient market hypothesis)。这个假说指出,在任何时候,股票的价格都反映了所有的相关信息,未来的价格必定遵循随机游走。有效市场假说依赖于一个自相矛盾的逻辑。因为要确定准确的价格需要付出时间和精力,财务分析师必须收集数据并构建模型。如果价格真的是随机游走的,所有这类活动都将无法得到预期的回报。然而,如果真的没有任何人花费时间和精力去估计价格,那么价格就会变得不准确,也就意味着人行道上会铺满百元钞票。
简而言之,如果投资者相信有效市场假说,他们就会停止分析,从而导致市场效率低下;而如果投资者认为市场效率低下,他们就会应用模型进行分析,从而提高市场效率。
事实上,股票市场上的价格变动与随机游走确实相当接近,尽管利用复杂的统计技术确实能够揭示某些短期模式。
从长远来看,有效市场假说或类似的假说是合理的。但是从短期来看,押注价格修正却可能存在不小的风险。不要过分相信一个模型。
小结
事实上,股票市场上的价格变动与随机游走确实相当接近,尽管利用复杂的统计技术确实能够揭示某些短期模式。
伟大的企业确实会拥有一些共同特征,但这个事实并不意味着这些特征就必定有助于成功。也许,很多表现糟糕的公司也拥有这些特征。挑选一些看上去很好的公司出来,列出它们的特征,这并不是模型思维。模型思维的要求是,推导出能够导致成功的那些特征,例如才华横溢的工人,然后再根据数据来检验相关结论。如果可能的话,最好寻找一些自然实验,也就是相关特征随机变化的实例。
在得出一般性的结论之前,必须应用多个模型,以避免“犯大错”的风险。也应该注意避免被某些“模式”所惑,看上去似乎是一个趋势,其实可能是随机。