局部多数模型
局部多数模型假设元胞是排列在棋盘上的。每个元胞处于两种状态中的一种:开或关。初始时,我们随机地给元胞分配状态,此后,元胞的状态取决于它“邻居”的状态。邻居可以通过多种方式加以定义。我们将元胞C的邻居定义为位于它东、南、西、北的4个元胞以及4个对角上的相邻元胞,因此它的领域大小为8。
局部多数模型
二维方格上的每个单元都处于两种状态之一:开或关。每个单元有8个邻居。在每个周期中,随机选择一个元胞。3当且仅当其中它的5个或更多邻居处于另一个状态时,这个元胞才会改变自己的状态。
局部多数模型中的局部互动包括正反馈:元胞要与其他元胞的状态相匹配。下图显示了局部多数模型的典型均衡配置。

在均衡状态下,每个元胞的状态都与它的大多数邻居的状态相匹配。虽然均衡配置取决于各元胞的初始配置,但是该模型对初始条件没有表现出极高的敏感性。改变一个元胞的状态最多只会导致最终配置出现很小的变化。最终的模式还取决于元胞被激活的顺序。因此,这个模型也表现出了路径依赖。它的均衡数量非常巨大,各个均衡之间的相似度也很低。
在局部多数模型的物理解释中,斑块状均衡模式对应于受挫状态(frustrated state)。可以把这种受挫状态理解为次优均衡(suboptimal equilibrium)。
比如,如果开对应于以握手的方式表示欢迎、关对应于以鞠躬的方式表示欢迎,那么位于“斑块”边界上的人在与他们的邻居互动时可能会碰到一些尴尬的情况:当其他人准备握手时他们却准备鞠躬,或者当其他人准备鞠躬时他们却准备握手。
相反,如果元胞是根据全局多数原则来匹配的,那么很快所有元胞都会处于相同的状态。这种观点意味着,创建共同行为可能需要影响更加广泛的网络。如果人们只在局部与自己的邻居协调,他们就会创造出各种各样的行为。因此矛盾的是,恰恰是协调导致了多样性。
纯粹协调博弈
在纯粹协调博弈(pure coordination games)中,每个博弈参与者都要在两个行动A或B中选择一个。如果两个博弈参与者都选择了相同的行动,那么每个博弈参与者的收益为1。如果两个人各自选择了不同的行动,那么每个人的收益都为0。
可以从纯粹协调博弈的角度重新解释局部多数模型:在这个博弈中,每个元胞都是一个博弈参与者,它必须选择一个共同行动来对抗它的8个邻居。如果博弈参与者只有在随机激活时才能改变行动,那么某个博弈参与者就可以通过选择与它的大多数邻居所选择的行动相匹配的行动来增加自己的收益。这种策略被称为短视最优响应(myopic best response),因为它没有考虑到邻居可能的未来行为。
一个博弈参与者有5个邻居选择了B,那么这个博弈参与者可以通过从A切换到B来在短期内增加自己的收益,但是,如果这个博弈参与者和邻居是被其他选择A的博弈参与者的“海洋”所包围的一个孤岛,那么这个博弈参与者保持A不变反而可能获得更高的期望收益。
协调的悖论
如果人们是在局部进行协调的,那么从全局的角度来看,整体配置将会是斑块状的、多样性的。
协调的悖论(paradox of coordination)将不同群体之间的差异解释为一种特异性的分歧。这种多样性有可能使我们的生活丰富多彩,也有可能变得非常低效。
在局部互动模型中,均衡时形成的斑块大小增加得比邻域的大小更快。如果我们使邻域,也就是影响网格上一个格子的格子数量增加到原来的两倍,那么斑块会变得比原来的两倍还大。因此,这个模型表明,当技术和城市化使人与人之间的联系更加紧密之后,协调的力量可以产生更大的同质性行为和信念。
生命游戏
生命游戏与局部多数模型的关键区别在于,元胞的更新规则有两个阈值,并且所有的元胞都同步更新自己的状态。
生命游戏
方格上的每个元胞都或者是活的(开的)或者是死的(关的)。每个元胞的邻居由网格上的8个相邻元胞组成。元胞根据如下两个规则同步更新自己的状态:
活的规则:对于一个死元胞,当恰好有三个活的邻居时,这个死元胞就会变活。
死的规则:对一个活元胞,当活的邻居小于两个时或当有三个以上的活邻居死去时,这个活元胞就会死去。
我们从排在同一条水平线上的三个活的元胞开始讨论。在下一个时期,对每个元胞应用上述死活规则之后,我们会得到排在同一条垂直线上的三个元胞。中间的活元胞有两个活着的邻居,所以它还活着。两端的两个活元胞分别只有一个活的邻居,所以它们都死了。最后,中间的活元胞的上方和下方的元胞都变活了,因为这两个元胞分别各有三个活着的邻居。根据对称性,等再下一个时期更新后,又会回到三个元胞组成水平线的情形。如果继续迭代运用上述规则,模型就会在水平线与垂直线之间不断交替,这也就是说,它将会不断“闪烁”。

闪光灯是由元胞之间的互动产生的,而不能直接从假设中推导出来。复杂系统学者将这种宏观现象称为涌现。
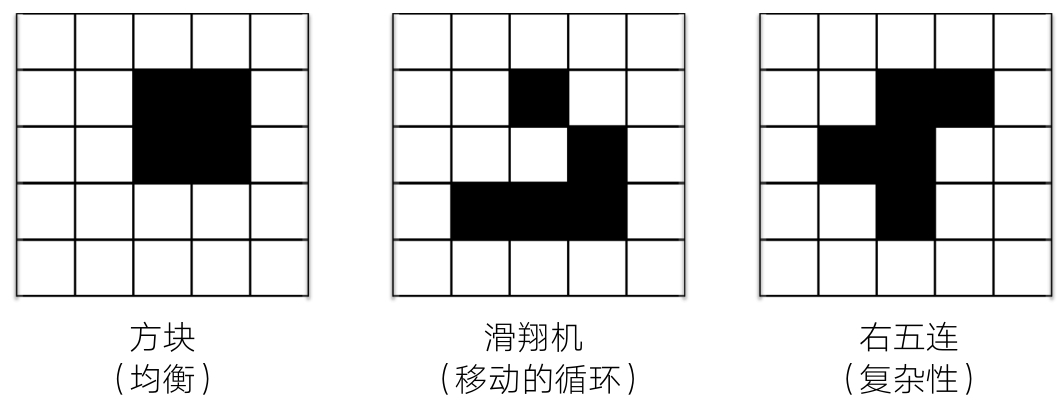
下图显示了其他三种简单涌现结构:方块、滑翔机和右五连(R-pentomino)。这是一个均衡配置;每个活元胞都有三个活的邻居,每个死元胞最多有两个活的邻居,因此,既没有活元胞死亡,也没有死元胞复活。
小结
局部多数模型,它总是可以达到某个均衡(尽管可能的均衡有许多种);生命游戏模型,能够产生从均衡到随机的任何一种类型的结果。
这个模型与现实世界之间不存在任何明确的联系。生命游戏给出了一个很好的例子,它说明,构建替代现实的模型是怎样帮助我们产生洞察力的,也就是从微观的规则中涌现出动态的宏观层面结构,这可以极大地加深我们对世界的理解。正如生命游戏所呈现的那样,整体可以执行远远超出其各个组成部分的功能。
生命游戏会产生复杂性,而局部多数模型则不可避免地走向均衡。
最后要强调的是,正是在我们对模型进行探索的过程中,才使模型(以及现实世界)是否会产生均衡、周期性、复杂性或随机性这个问题突显了出来。确实,模型既能够回答问题,也能够提出问题。它们关上了一些门,同时又打开了更多的门。