如果能够为模型构建一个李雅普诺夫函数,那么模型必定会达到均衡。在这种情况下,我们不可能得出周期性、随机性或复杂性。更重要的是我们甚至可以确定模型收敛到均衡所需的时间。
李雅普诺夫函数
给定一个离散时间动态系统,它的转移规则由xt+1=G(xt)组成。对于实值函数F(xt),如果对于所有的xt,都有F(xt)≥M,而且存在一个A>0,使得下式成立,那么这个实值函数F(xt)是李雅普诺夫函数:
F(xt+1)≤F(xt)-A,如果G(xt)≠xt
如果对于G,F是一个李雅普诺夫函数,那么从任何x0开始,必定存在一个t*,使G(xt*)=xt*,即该系统会在有限时间内达到均衡。
一个李雅普诺夫函数是从配置到实数的一个映射,它满足两个假设:第一,如果转移函数不处于均衡状态,则李雅普诺夫函数的值就会减少某个固定的数量;第二,李雅普诺夫函数具有最小值。如果这两个假设成立,那么该动态系统必定达到均衡。
逐底竞争博弈
有N个博弈参与者,每个博弈参与者在每个时期都要提出一个支持水平,其取值范围为{0,1,…,100}。提出了最接近平均支持水平2/3的博弈参与者可以获得那个期间的奖励。
这个博弈可以用来解释美国各州政府削减社会项目支出的行为,例如减少对贫困人口的援助。每个州都会提供一些资金,但只愿意提供低于平均水平的资金。
逐底竞争博弈是否能达到均衡,取决于博弈参与者的行为规则。如果博弈参与者随机选择支持水平,那么结果就将会是随机的。然而,考虑到这个博弈的收益结构,随机选择支持水平并没有意义。在这里,我们假设如下行为规则,这种规则与实验研究的结果一致。在第一个时期,我们假设每个博弈参与者会随机选择一个低于50的支持水平。在以后各期中,每个博弈参与者选择的水平至少等于1且低于上一期平均水平的2/3。如果上一期的平均水平已经小于零,那么每个博弈参与者都会选择零。
另外,假设我们允许博弈参与者在0至100的区间内选择任何实数值,而不是整数值。再假设在每一轮中,博弈参与者选择的支持水平等于上一轮平均水平的2/3,那么平均支持水平将会随着时间的推移而逐渐降低,但是永远不会达到零的均衡。正如色诺悖论(Xeno’s paradox)一样,这个过程会越来越接近于零,但是却永远不会达到零。因此,为了确保均衡的实现,还必须假设一个最小减量(A)。
局部多数模型
我们将局部多数模型中的李雅普诺夫函数定义为总体中的总不一致性(total disagreement),即与相反状态的元胞相邻的所有元胞数量的总和。为了证明这个模型必定会达到均衡,我们必须先证明,如果一个元胞改变了自己的状态,那么总不一致性至少会下降一个固定的数量。
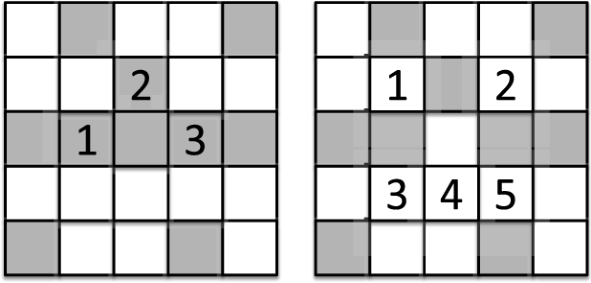
首先,如果一个元胞改变了自己的状态,那么相对于它的邻居而言它必定是少数。它至少有5个邻居处于相反状态,最多有3个邻居处于相同状态。因此,当这个元胞切换状态后,与这个元胞不一致的元胞数量至少减少了两个。为了计算总不一致性的变化,还必须将与这个元胞相邻的元胞对总不一致性变化的贡献考虑进去。由此,那5个或更多的现在状态一致的元胞的不一致性减少了(每个元胞减少1),同时之前状态一致的那3个或更少的元胞现在则具有更高的不一致性了(每个元胞增加1)。因此,所有相邻元胞的总不一致性至少下降了4。
这样一来,我们就证明了,即使某些元胞可能带来更多的不一致性,总不一致性也满足李雅普诺夫函数的条件。因此,局部多数模型必定会收敛到均衡,不仅仅是有些时候或大部分时候,而是所有时间都是如此。我们还可以确定收敛的速度:无论什么时候一个元胞改变自身的状态,总不一致性至少会下降4。由此可知,一个总一致性为100的配置,必定会在25个时期内达到均衡。换句话说,一个总一致性为D的配置,必定会在D/4个时期内达到均衡。正如我们在第15章中已经指出过的,实现的均衡几乎总是一个低效率的斑块状模式,它包括了不少受挫的元胞。
自组织活动模型
自组织活动模型中也存在均衡。这个模型中由一群人和每个人可以选择去做的活动的集合组成。这个模型的关键假设是,每个人都更偏好不那么拥挤的活动,例如,更少人参加同一项活动意味着在健身房不用等待、在面包店和咖啡店不用排队。
一个城市里,有A种活动可以参加,每一天都由L个时间段组成。在人口规模为M的城市中,每个人都要选定一个日程安排。在这里,日程安排是指这个人在L个时间段内分配L种活动(从一个更大的K种可能性的集合中)。一个人要面对的拥挤水平则设定为等于同时选择同一种活动的其他人的数量。
为了证明这个模型是收敛的,我们要证明总拥挤度(total congestion),也就是整个人群拥挤水平的总和满足李雅普诺夫函数的条件。当一个人降低了他的拥挤水平时,就会降低自己对总拥挤度的贡献,并且会使他不再遇到的每个人的拥挤水平减少1,同时使他新遇到的每一个人的拥挤水平增加1。既然他降低了自己的拥挤水平,第一组人的数量会比第二组人更多。
例如,假设一个人原本在早上8点去一个拥挤的健身房,在下午4点去一个拥挤的咖啡馆,如果她改为在上午8点去咖啡馆,并在下午4点去健身房,结果发现在上午8点那个时段咖啡馆几乎是全空的,健身房在下午4点时只是有一点点拥挤,那么她降低了自己以及之前遇到的所有人的拥挤水平。她确实使她现在遇到的少数人提高了拥挤水平,但是总拥挤度却下降了(而且至少减少了1)。既然总拥挤度不可能低于零,系统必定会达到均衡。
虽然,一般来说,我们无法保证系统能够找到一个有效率的均衡,但是这种自组织活动模型几乎总能收敛到总拥挤度近乎最小的配置。而在效率低下的配置中,更多人选择在同一个时间段参加某一项活动(比如去健身房),而不是去参加另一项活动(比如去咖啡馆)。如果在这两项活动中拥挤程度的差异很大,那么一个人就可以通过切换自己去健身房和咖啡馆的时间来降低拥挤水平。
这个模型可以解释当今世界的很多秩序,它可以让我们更加深刻地理解城市如何在没有中央计划者的情况下通过自组织实现近乎完全有效的配置。但是对于许多游乐园,比如迪斯尼,却做不到这一点。因为新的参观者没有时间去尝试新的路线。
李雅普诺夫函数在交易环境中是否存在,取决于负外部性的大小。但是外部性(即便是负外部性)的存在,不能排除构建李雅普诺夫函数的需要。局部多数模型和路径选择模型都包含了负外部性。在局部多数模型中,当一个元胞改变了自己状态时,它会对处于相反状态的邻居施加负外部性。然而,它与现在匹配的邻居产生的正外部性更大。
小结
李雅普诺夫函数不仅可以帮助我们证明一个系统或模型能不能达到均衡,还可以告诉我们达到均衡的速度有多快。
同时,如果我们不能构建一个总是减少或总是增加的全局变量,那么,就无法保证这些过程能够达到均衡。
回顾一下模型的7大用途——推理、解释、设计、沟通、行动、预测和探索,我们就会发现李雅普诺夫函数在每个用途上都有所帮助。如上所述,利用李雅普诺夫函数,我们可以推断出系统走向均衡的原因,还可以解释系统收敛到均衡的速度、设计信息系统(例如迪斯尼世界所采取的分时段游览的预约系统)、采取行动(例如对办公桌进行交易是不可取的)、沟通系统如何达到均衡的途径、预测系统达到平衡的时间以及进行探索。我们可以尝试提出假设和构建模型来解释一些令人惊讶的现象,例如自组织的城市。